Available under Creative Commons-ShareAlike 4.0 International License.
In classical physics, the kinetic energy Kof an object of mass m moving at velocity vis given by K= 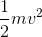 . For example, if a car is to start from a stoplight and then accelerate up to
v, this is the theoretical minimum amount of energy that would have to be used up by burning gasoline. (In reality, a car’s engine is not 100% efficient, so the amount of gas burned is
greater.) Einstein’s theory of relativity states that the correct equation is actually
. For example, if a car is to start from a stoplight and then accelerate up to
v, this is the theoretical minimum amount of energy that would have to be used up by burning gasoline. (In reality, a car’s engine is not 100% efficient, so the amount of gas burned is
greater.) Einstein’s theory of relativity states that the correct equation is actually
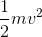 . For example, if a car is to start from a stoplight and then accelerate up to
v, this is the theoretical minimum amount of energy that would have to be used up by burning gasoline. (In reality, a car’s engine is not 100% efficient, so the amount of gas burned is
greater.) Einstein’s theory of relativity states that the correct equation is actually
. For example, if a car is to start from a stoplight and then accelerate up to
v, this is the theoretical minimum amount of energy that would have to be used up by burning gasoline. (In reality, a car’s engine is not 100% efficient, so the amount of gas burned is
greater.) Einstein’s theory of relativity states that the correct equation is actually
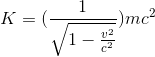
where c is the speed of light. The fact that it diverges as v→c is interpreted to mean that no object can be accelerated to the speed of light.2 2 X
(4k)!(1103 + 26390k) Expand K in a Taylor series, and show that the first nonvanishing term is equal to the classical expression. This means that for velocities that
are small compared to the speed of light, the classical expression is a good approximation, and Einstein’s theory does not contradict any of the prior empirical evidence from which the
classical expression was inferred.
- 瀏覽次數:2009






