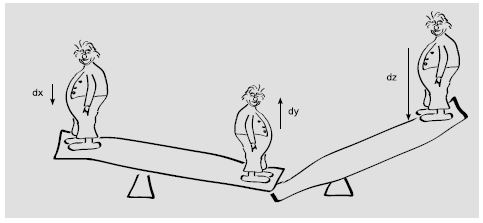
Figure 2.9 shows three
clowns on seesaws. If the leftmost clown moves down by a distance 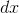 ,
the middle one will come up by
,
the middle one will come up by 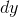 , but this will also cause the one on
the right to move down by
, but this will also cause the one on
the right to move down by 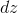 . If we want to predict how much the
rightmost clown will move in response to a certain amount of motion by the leftmost one, we have
. If we want to predict how much the
rightmost clown will move in response to a certain amount of motion by the leftmost one, we have
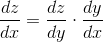
This is called the chain rule. It says that if a change in 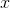 causes
causes
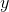 to change, and
to change, and 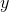 then
causes
then
causes  to change, then this chain of changes has a cascading effect.
Mathematically, there is no big mystery here. We simply cancel
to change, then this chain of changes has a cascading effect.
Mathematically, there is no big mystery here. We simply cancel 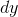 on the
top and bottom. The only minor subtlety is that we would like to be able to be sloppy by using an expression like
on the
top and bottom. The only minor subtlety is that we would like to be able to be sloppy by using an expression like 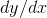 to mean both the quotient of two infinitesimal numbers and a derivative, which is defined as the standard part of this quotient.
This sloppiness turns out to be all right, as proved in Proof
of the chain rule.
to mean both the quotient of two infinitesimal numbers and a derivative, which is defined as the standard part of this quotient.
This sloppiness turns out to be all right, as proved in Proof
of the chain rule.
Example
Jane hikes 3 kilometers in an hour, and hiking burns 70 calories per kilometer. At what rate does she burn calories?
We let 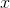 be the number of hours she’s spent hiking so far,
be the number of hours she’s spent hiking so far, 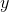 the distance covered, and
the distance covered, and  the calories spent. Then
the calories spent. Then
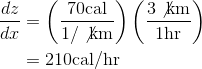
Example
Figure 2.10 shows a piece of farm equipment containing a train of gears with 13, 21, and 42 teeth. If the smallest gear is
driven by a motor, relate the rate of rotation of the biggest gear to the rate of rotation of the motor.
Let x, y, and z be the angular positions of the three gears. Then
by the chain rule,
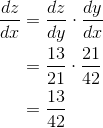

The chain rule lets us find the derivative of a function that has been built out of one function stuck inside another.
Example
Find the derivative of the function 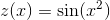 .
.
Let 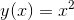 , so that
, so that 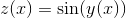 . Then
. Then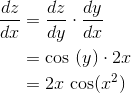 The way people usually say it is that the chain rule tells you to take the derivative of the
outside function, the sine in this case, and then multiply by the derivative of “the inside stuff,” which here is the square. Once you get used to doing it, you don’t need to invent a third,
intermediate variable, as we did here with
The way people usually say it is that the chain rule tells you to take the derivative of the
outside function, the sine in this case, and then multiply by the derivative of “the inside stuff,” which here is the square. Once you get used to doing it, you don’t need to invent a third,
intermediate variable, as we did here with  .
.
Example
Let’s express the chain rule without the use of the Leibniz notation. Let the function  be defined by
be defined by 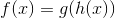 . Then the derivative of
. Then the derivative of 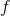 is given by
is given by 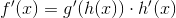
Example
We’ve already proved that the derivative of 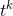 is
is 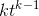 for
for 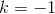 (Example) and for
(Example) and for 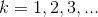 (Derivatives of polynomials). Use these facts to extend the
rule to all integer values of
(Derivatives of polynomials). Use these facts to extend the
rule to all integer values of 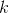 .
.
For 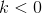 , the function
, the function 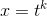 can be written as
can be written as 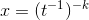 , where
, where 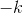 is positive. Applying the chain rule, we find
is positive. Applying the chain rule, we find 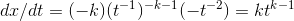 .
.
- 瀏覽次數:4135






