To prove that l’Hˆopital’s rule works in general for ∞/∞forms, we do a change of variable on the outputs of the functions uand vrather than their inputs. Suppose that our original problem is of the form
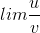
where both functions blow up. 1 We then
de ne U = 1=u and V = 1=v. We now have
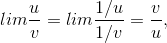
and since Uand V both approach zero, we have reduced the problem to one that can be solved using the version of l’Hˆopital’s rule already proved for indeterminate forms like 0/0. Differentiating and applying the chain rule, we have
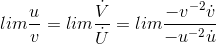
Since lim ab= lim a lim b provided that lim aand lim bare both defined, we can rearrange factors to produce the desired result.
This change of variable is a specific example of a much more general method of problem-solving in which we look for a way to reduce a hard problem to an easier one. We will encounter changes of variable again on p. 87 as a technique for integration, which means undoing the operation of differentiation.
- 瀏覽次數:1877






