Given a function like
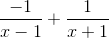
we can rewrite it over a common denominator like this:
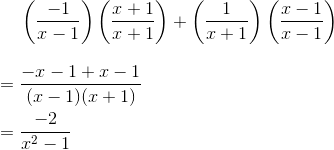
But note that the original form is easily integrated to give
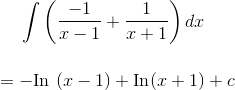
While faced with the form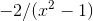 
, we wouldn’t have known how to
integrate it.
Note that the original function was of the fo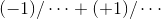rm 
It’s not a coincidence that the two constants on top,
−1 and +1, are opposite in sign but equal in absolute value. To see why, consider the behavior of this function for large values of x. Looking at the form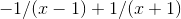 
, we might naively guess that for a large value of 
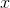such as 1000, it would come out to be somewhere on the order thousandths. But looking at
the form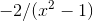 
, we would expect it to be way down in the
millionths. This seeming paradox is resolved by noting that for large values of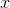 
, the two terms in the form 
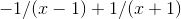very nearly cancel. This cancellation could only have happened if the constants on top were opposites like plus and minus
one.
The idea of the method of partial fractions is that if we want to do an integral of the form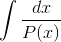
where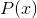 
is an nth order polynomial, we rewrite 
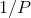as
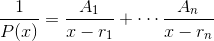
where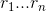 
are the roots of the polynomial, i.e., the solutions of
the equation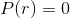 
. If the polynomial is second-order, you can find
the roots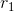 
and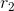 
using the quadratic formula; I'll assume for the time being that they're real. For
higher-order polynomials, there is no surefire, easy way of finding the roots by hand, and you'd be smart simply to use computer software to do it. In Yacas, you canfind the real roots of a
polynomial like this:
FindRealRoots(x^4-5*x^3 -25*x^2+65*x+84) f3.,7.,-4.,-1.g
(I assume it uses Newton's method to nd them.) The constants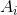 
can then be determined by algebra, or by the following trick.
- 瀏覽次數：2335
