Here we prove, as claimed, that the form of Generalizations of l’Hoˆpital’s rule can be generalized to the case where more than one application of the rule is required. The proof requires material from (Integration), and, as discussed in Example 86 , the motivation for the result becomes much more transparent once has read and knows about Sequences and Series. The reader who has arrived here while reading Limits and continuity will need to defer reading this section of the proof until after Integration, and may wish to wait until after Sequences and Series.
The proof can be broken down into two steps.
Step 1: We first have to establish a stronger form of l’Hˆopital’s rule that states that lim u/v= lim 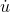 /
/ 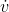 rather than lim u/v =
rather than lim u/v = 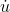 /
/ 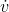 . This form is stronger, because in a case like Example ,
. This form is stronger, because in a case like Example , 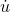 /
/ 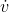 isn’t defined, but lim
isn’t defined, but lim 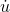 /
/ 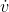 is.
is.
We prove the stronger form using the The mean value theorem. For simplicity of notation, let’s assume that the limit is being taken at x= 0.
By the fundamental theorem of calculus, we have u(x) = R x 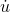 (x0) dx0
(x0) dx0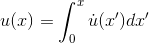 , and the mean value theorem then tells us that for some pbetween 0 and x, u(x) =
x
, and the mean value theorem then tells us that for some pbetween 0 and x, u(x) =
x 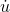 (p). Likewise for a qin
this interval, v(x) = x
(p). Likewise for a qin
this interval, v(x) = x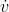 (q). So
(q). So
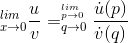
but since both pand q are closer to zero than xis, the limit as they simultaneously approach zero is the same as the limit as xapproaches zero.
Step 2: If we need to take nderivatives, the proof follows by applying the extra-strength rule ntimes. 1
- 瀏覽次數:2056






