An expression like 0/0, called an indeterminate form, can be thought of in a different way in terms of infinitesimals. Suppose I tell you I have two infinitesimal numbers 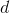 and
and  in my pocket, and I ask you whether
in my pocket, and I ask you whether 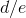 is finite, infinite, or infinitesimal. You can't tell, because
is finite, infinite, or infinitesimal. You can't tell, because 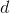 and
and  might not be infinitesimals of the same order of magnitude. For instance, if
might not be infinitesimals of the same order of magnitude. For instance, if
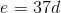 , then
, then 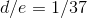 is finite; but if
is finite; but if 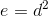 , then
, then 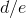 is infinite; and if
is infinite; and if 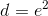 , then d/e is infinitesimal. Acting this out
with numbers that are small but not infinitesimal,
, then d/e is infinitesimal. Acting this out
with numbers that are small but not infinitesimal,
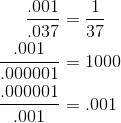
On the other hand, suppose I tell you I have an infinitesimal number 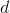 and a finite number
and a finite number 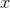 , and I ask you to speculate about
, and I ask you to speculate about 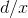 . You know for sure that it's going to be infinitesimal. Likewise, you can be sure
that
. You know for sure that it's going to be infinitesimal. Likewise, you can be sure
that 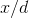 is infinite. These aren't indeterminate forms.
is infinite. These aren't indeterminate forms.
We can do something similar with infinite numbers. If 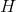 and
and 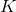 are both infinite, then
are both infinite, then 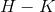 is indeterminate. It could be infinite, for example, if
is indeterminate. It could be infinite, for example, if 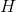 was positive infinite and
was positive infinite and 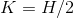 . On the other hand, it could be finite if
. On the other hand, it could be finite if 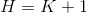 . Acting this out with big but finite numbers,
. Acting this out with big but finite numbers,
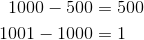
Example
If 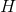 is a positive infinite number, is
is a positive infinite number, is 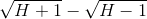 finite, infinite, infinitesimal, or indeterminate?
finite, infinite, infinitesimal, or indeterminate?
Trying it with a finite, big number, we have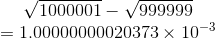
: H=1/d d^-1 : sqrt(H+1)-sqrt(H-1) d^1/2+0.125d^5/2+...
For convenience, the first line of input defines an infinite number 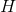 in terms of the calculator’s built-in infinitesimal
in terms of the calculator’s built-in infinitesimal 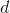 . The result has only positive powers of
. The result has only positive powers of 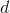 , so it’s clearly
infinitesimal.
, so it’s clearly
infinitesimal.
More rigorously, we can rewrite the expression as 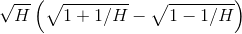 . Since the derivative of the square root function
. Since the derivative of the square root function 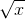 evaluated at
evaluated at 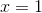 is
is 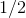 , we can approximate this as
, we can approximate this as
![\sqrt{H}\left [ 1+\frac{1}{2H}+...-\left ( 1-\frac{1}{2H}+... \right ) \right ]\\ \begin{align*} &= \sqrt{H}\left [ \frac{1}{H}+... \right ]\\ &=\frac{1}{\sqrt{H}} \end{align*}](/system/files/resource/33/33298/33537/media/eqn-img_33.gif) which is infinitesimal.
which is infinitesimal.
- 瀏覽次數:3884






