You are here

Home » Operations Management » Reliability and Maintainability in Operations Management

Fleet reliability

15 January, 2016 - 09:25
Available under Creative Commons-ShareAlike 4.0 International License.

Suppose you have studied the reliability of a component, and found that it is 80% for a mission duration of 3 hours. Knowing that we have 5 identical items simultaneously active, we might be interested in knowing what the overall reliability of the group would be. In other words, we want to know what is the probability of having a certain number of items functioning at the end of the 3 hours of mission. This issue is best known as fleet reliability.

Consider a set of midentical and independent systems in a same instant, each having a reliability R. The group may represent a set of systems in use, independent and identical, or could represent a set of devices under test, independent and identical. A discrete random variable of great interest reliability is N, the number of functioning items. Under the assumptions specified, N is a binomial random variable, which expresses the probability of a Bernoulli process. The corresponding probabilistic model is, therefore, the one that describes the extraction of balls from an urn filled with a known number of red and green balls. Suppose that the percentage R of green balls is coincident with the reliability after 3 hours. After each extraction from the urn, the ball is put back in the container. Extraction is repeated m times, and we look for the probability of finding n green. The sequence of random variables thus obtained is a Bernoulli process of which each extraction is a test. Since the probability of obtaining N successes in mextractions from an urn, with restitution of the ball, follows the binomial distribution B(m,R)B, the probability mass function of N is the well-known:

   
P\left ( N=n \right )=\frac{m!}{n!\left ( m-n \right )!}R^{n}\left ( 1-R \right )^{m-n}    

The expected value of N is given by: E(N)=μN=m∙R and the standard deviation is:

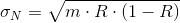
\sigma _{N}=\sqrt{m\cdot R\cdot \left ( 1-R \right )}

Let’s consider, for example, a corporate fleet consisting of 100 independent and identical systems. All systems have the same mission, independent from the other missions. Each system has a reliability of mission equal to 90%. We want to calculate the average number of missions completed and also what is the probability that at least 95% of systems would complete their mission. This involves analyzing the distribution of the binomial random variable characterized by R = 0.90 and m = 100. The expected value is given by E(N)=μN=100∙0.9=90.

The probability that at least 95% of the systems complete their mission can be calculated as the sum of the probabilities that complete their mission 95, 96, 97, 98, 99 and 100 elements of the fleet:

  
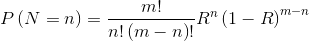
P\left ( N\geq n \right )=\sum_{n=95}^{100} [ \frac{m!}{n!( m-n )!} R^{n} ( 1-R )^{m-n}]=0,058    

  • 1343 reads