A second special case of the general model of minimal repair, is obtained if the failure time T is a random variable with a Weibull distribution, with shape parameter β and scale parameter α.
In this case the sequence of failure times is described by a Non-Homogeneous Poisson Process - NHPP with intensity z(t) equal to the probability density function of the Weibull distribution:
|
|
Since the cumulative intensity of the process is defined by:
|
|
the cumulative function is:
|
|
As it can be seen, the average number of faults occurring within the time t≥0 of this not homogeneous poissonian process E[N(t)]=Z(t), follows the so-called power law.
If β>1, it means that the intensity function z(t) increases and, being this latter the expression of the average number of failures, it means that faults tend to occur more frequently over time. Conversely, if β<1, faults decrease over time.
In fact, if we take α=10 hours (λ=0.1 failures/h) and β=2, we have:
![E\left [ N\left ( 100 \right ) \right ]=\left ( 0.1\cdot 100 \right )^{2}=100=10^{2};\\ E\left [ N\left ( 1000 \right ) \right ]=\left ( 0.1\cdot 1000 \right )^{2}=10000=100^{2};\\E\left [ N\left ( 10000 \right ) \right ]=\left ( 0.1\cdot 10000 \right )^{2}=1000000=1000^{2}](/system/files/resource/18/18769/18986/media/eqn-img_4.gif) .
.
We can observe a trend no longer linear but increasing according to a power law of a multiple of the time width considered.
The probability mass function of N(t) thus becomes:
|
|
For example, let us consider a system that fails, according to a power law, having β=2.2 and α=1500 hours. What is the average number of faults occurring during the first 1000 hours of operation? What is the probability of having two or more failures during the first 1000 hours of operation? Which is the average number of faults in the second 1000 hours of operation?
The average number of failures that occur during the first 1000 hours of operation, is calculated with the expected value of the distribution:
|
|
The probability of two or more failures during the first 1000 hours of operation can be calculated as complementary to the probability of having zero or one failure:
|
|
The average number of faults in the succeeding 1000 hours of operation is calculated using the equation:
|
|
that, in this case, is:
|
|
- 1984 reads





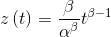
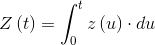
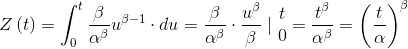
![P\left [ N\left ( t \right ) =n\right ]=\frac{Z\left ( t \right )^{n}}{n!}e^{-Z\left ( t \right )}=\frac{\frac{t}{\alpha }^{\beta \cdot n}}{n!}e^{-\frac{t}{\alpha }^{\beta }}](/system/files/resource/18/18769/18986/media/eqn-img_5.gif)
![E\left [ N\left ( t \right ) \right ]=\mu _{N\left ( t \right )}=Z\left ( t \right )=\left ( \frac{t}{\alpha } \right )^{\beta }\rightarrow E\left [ N\left ( 1000 \right ) \right ]=\left ( \frac{1000}{1500} \right )^{2.2}=0.41](/system/files/resource/18/18769/18986/media/eqn-img_6.gif)
![P\left [ N\left ( 1000 \right )\geq 2 \right ]=1-P\left [ N\left ( 1000 \right ) < 2\right ]=1-\sum_{n=0}^{1}\frac{\left ( \frac{t}{\alpha } \right )^{\beta \cdot n}}{n!}e^{-\frac{t}{\alpha }^{\beta }}\\=1-\frac{0.41^{0}}{0!}e^{-0.41}-\frac{0.41^{1}}{1!}e^{-0.41}=1-0.663-0.272=0.064](/system/files/resource/18/18769/18986/media/eqn-img_7.gif)
![E\left [ N\left ( t+s \right )-N\left ( s \right ) \right ]=Z\left ( t+s \right )-Z\left ( s \right )](/system/files/resource/18/18769/18986/media/eqn-img_8.gif)
![E\left [ N\left ( 2000 \right )-N\left ( 1000 \right ) \right ]=Z\left (2000 \right )-Z\left (1000 \right )=1.47](/system/files/resource/18/18769/18986/media/eqn-img_9.gif)

