After seeing the main definitions of reliability and maintenance, let's finally see how we can use reliability knowledge also to carry out an economic optimization of replacement activities.
Consider a process that follows the power law with β>1. As time goes by, faults begin to take place more frequently and, at some point, it will be convenient to replace the system.
Let us define with τ the time when the replacement (here assumed instantaneous) takes place. We can build a cost model to determine the optimal preventive maintenance time τ* which optimizes reliability costs.
Let’s denote by Cf the cost of a failure and with Cr the cost of replacing the repairable system.
If the repairable system is replaced every τ time units, in that time we will have the replacement costs Cr and so many costs of failure Cf as how many are the expected number of faults in the time range(0;τ]. The latter quantity coincides with the expected value of the number of faults E[N(τ)].
The average cost per unit of time c(τ), in the long term, can then be calculated using the following relationship:
|
|
Then follows:
|
|
Differentiating c(τ) with respect to τ and placing the differential equal to zero, we can find the relative minimum of costs, that is, the optimal time τ* of preventive maintenance. Manipulating algebraically we obtain the following final result:
|
|
Consider, for example, a system that fails according to a Weibull distribution with β=2.2 and α=1500 hours. Knowing that the system is subject to replacement instantaneous and that the cost of a fault Cf=2500 € and the cost of replacing Cr=18000 €, we want to evaluate the optimal interval of replacement.
The application of Table 4.8 provides the answer to the question:
|
|
- 2203 reads





![c\left ( \tau \right )=\frac{C_{f}\cdot E\left [ N\left ( \tau \right ) \right ]+C_{r}}{\tau }](/system/files/resource/18/18769/18987/media/eqn-img_1.gif)
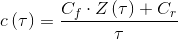
![\tau^{\ast }= \alpha \cdot \left [ \frac{C_{r }}{C_{f}\left ( \beta -1 \right )} \right ]^{\frac{1}{\beta }}](/system/files/resource/18/18769/18987/media/eqn-img_3.gif)
![\tau^{\ast }= \alpha \cdot \left [ \frac{C_{r }}{C_{f}\left ( \beta -1 \right )} \right ]^{\frac{1}{\beta }}=1500\cdot \left [ \frac{18000}{2500\left ( 2.2-1 \right )} \right ]^{\frac{1}{2.2}}\\=1500\cdot 2.257= 3387\left [ \textrm{h} \right ]](/system/files/resource/18/18769/18987/media/eqn-img_4.gif)

