Minimal repair with CFR

Available under Creative Commons-ShareAlike 4.0 International License.

A well-known special case of the general model of minimal repair, is obtained if the failure time T is a random variable with exponential distribution, with failure rate λ.

In this case, the general model of minimal repair is simplified because the number E[N(t)] of faults that occur within the time t: {N(t), t≥0} is described by a homogeneous Poisson process with intensity z(t)=λ, and is:

$E\left [ N\left ( t \right ) \right ]=\mu _{N\left ( t \right )}= Z\left ( t \right )= \int_{0}^{t}z\left ( u \right )\cdot du= \int_{0}^{t}\lambda\cdot du = \lambda t$

If, for example, we consider λ=0.1 faults/hour, we obtain the following values at time 100, 1000 and 10000: $E\left [ N\left ( 100 \right ) \right ]=0,1\cdot 100=10;\; E\left [ N\left ( 1000 \right ) \right ]=0,1\cdot 1000=100;$ $E\left [ N\left ( 10000 \right ) \right ]=0,1\cdot 10000=1000$ It should be noted, as well, a linear trend of the expected number of failures given the width of the interval taken.

Finally, we can obtain the probability mass function of N(t), being a Poisson distribution:

$P\left [ N\left ( t \right ) =n\right ]=\frac{Z\left ( t \right )^{n}}{n!}e^{-Z\left ( t \right )}= \frac{\left ( \lambda t \right )^{n}}{n!}e^{-\lambda t}$

Also, the probability mass function of N(t+s)−N(s), that is the number of faults in a range of amplitude t shifted forward of s, is identical:

$P\left [ N\left ( t +s\right ) -N\left ( s \right )=n\right ]=\frac{\left ( \lambda t \right )^{n}}{n!}e^{-\lambda t}$

Since the two values are equal, the conclusion is that in the homogeneous Poisson process (CFR), the number of faults in a given interval depends only on the range amplitude.

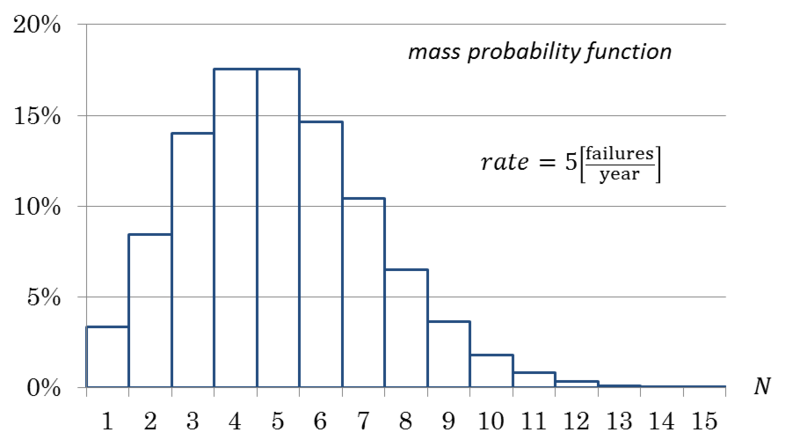
The behavior of a Poisson mass probability distribution, with rate equal to 5 faults each year, representing the probability of having n∈N faults within a year, is shown in Figure 4.18.

Figure 4.18 Poisson distribution

In the diagram you can see the probability of having N faults within a year, having a homogeneous Poisson process with a rate of 5 faults each year.

Since in the model of minimal repair with CFR, repair time is supposed to be zero (MTTR = 0), the following relation applies:

$MTBF=MTTF+MTTR=MTTF=\frac{1}{\lambda }$

Suppose that a system, subjected to a repair model of minimal repair, shows failures according to a homogeneous Poisson process with failure rate λ= 0.0025 failures per hour. We’d like to estimate the average number of failures that the system will have during 5000 hours. Then, determine the probability of having not more than 15 faults in a operation period of 5000 hours.

The estimate of the average number of failures in 5000 hours, can be carried out with the expected value function:

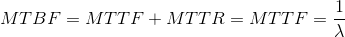
$E\left [ N\left ( t \right ) \right ]=\lambda \cdot t\rightarrow E\left [ N\left ( 5000 \right ) \right ]=0.0025\left [ \frac{\textrm{failures}}{\textrm{h}} \right ]\cdot 5000\left [ \textrm{h} \right ]=12.5\left [\textrm{ failures} \right ]$

The probability of having not more than 15 faults in a period of 5000 hours of operation, is calculated with the sum of the probability mass function evaluated between 0 and 15:

$P\left [ N\left ( 5000 \right )\leq 15 \right ]=\sum_{n=0}^{15}\frac{\left (\lambda t \right )^{n}}{n!}e^{-\lambda\cdot t}= \sum_{n=0}^{15}\frac{12.5^{n}}{n!}e^{-12.5}=0.806$

瀏覽次數：1343

您在這裡

Minimal repair with CFR