Intuitively, a continuous function is one whose graph has no sudden jumps in it; the graph is all a single connected piece. Such a function can be drawn without picking the pen up off of the
paper. Formally, a function 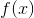 is defined to be continuous if for
any real
is defined to be continuous if for
any real 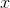 and any infinitesimal
and any infinitesimal 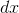 ,
, 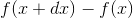 is infinitesimal.
is infinitesimal.
Example
Let the function 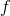 be defined by
be defined by 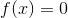 for
for 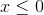 , and
, and 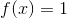 for
for 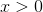 . Then f (x ) is discontinuous, since for dx > 0, f (0 + dx ) − f (0) = 1, which isn’t infinitesimal.
. Then f (x ) is discontinuous, since for dx > 0, f (0 + dx ) − f (0) = 1, which isn’t infinitesimal.

If a function is discontinuous at a given point, then it is not differentiable at that point. On the other hand, the example 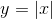 shows that a function can be continuous without being differentiable.
shows that a function can be continuous without being differentiable.
In most cases, there is no need to invoke the definition explicitly in order to check whether a function is continuous. Most of the functions we work with are de- fined by putting together
simpler functions as building blocks. For example, let’s say we’re already convinced that the functions defined by 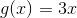 and
and 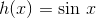 are both continuous. Then if we encounter the function
are both continuous. Then if we encounter the function 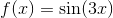 , we can tell that it’s continuous because its definition corresponds to
, we can tell that it’s continuous because its definition corresponds to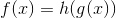 . The functions
. The functions 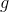 and
and 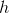 have been set up like a bucket brigade, so that
have been set up like a bucket brigade, so that 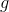 takes the
input, calculates the output, and then hands it off to
takes the
input, calculates the output, and then hands it off to 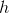 for the final step of the calculation. This method of combining functions is
called composition. The composition of two continuous functions is also continuous. Just watch out for division. The function
for the final step of the calculation. This method of combining functions is
called composition. The composition of two continuous functions is also continuous. Just watch out for division. The function 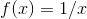 is continuous everywhere except at
is continuous everywhere except at 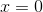 , so for example
, so for example 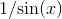 is continuous everywhere except at multiples of
is continuous everywhere except at multiples of 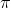 , where the sine has zeroes.
, where the sine has zeroes.
- 2914 reads






