Because any formula can be differentiated symbolically to find an- other formula, the main motivation for doing derivatives numerically would be if the function to be differentiated wasn’t known in symbolic form. A typical example might be a two-person network computer game, in which player A’s computer needs to figure out player B’s velocity based on knowledge of how her position changes over time. But in most cases, it’s numerical integration that’s interesting, not numerical differentiation.
As a warm-up, let’s see how to do a running sum of a discrete function using Yacas. The following program computes the sum 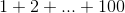 discussed to in Change in discrete steps. Now that we’re writing real computer programs with Yacas, it would be a good idea to enter each program into a file before trying to run it. In
fact, some of these examples won’t run properly if you just start up Yacas and type them in one line at a time. If you’re using Adobe Reader to read this book, you can do
discussed to in Change in discrete steps. Now that we’re writing real computer programs with Yacas, it would be a good idea to enter each program into a file before trying to run it. In
fact, some of these examples won’t run properly if you just start up Yacas and type them in one line at a time. If you’re using Adobe Reader to read this book, you can do  , select the program, copy it into a file, and
then edit out the line numbers.
, select the program, copy it into a file, and
then edit out the line numbers.
Example
n := 1; sum := 0; While (n<=100) [ sum := sum+n; n := n+1; ]; Echo(sum)
The semicolons are to separate one instruction from the next, and they become necessary now that we’re doing real programming. Line 1 of this program defines the variable n, which will take on
all the values from 1 to 100. Line 2 says that we haven’t added anything up yet, so our running sum is zero so far. Line 3 says to keep on repeating the instructions inside the square brackets
until n goes past 100. Line 4 updates the running sum, and line 5 updates the value of n. If you’ve never done any programming before, a statement like 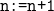 might seem like nonsense — how can a number equal itself plus one? But that’s why we use
the := symbol; it says that we’re redefining
might seem like nonsense — how can a number equal itself plus one? But that’s why we use
the := symbol; it says that we’re redefining 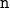 , not stating an
equation. If
, not stating an
equation. If 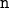 was previously 37, then after this statement is executed, n will be redefined
as 38. To run the program on a Linux computer, do this (assuming you saved the pro- gram in a file named
was previously 37, then after this statement is executed, n will be redefined
as 38. To run the program on a Linux computer, do this (assuming you saved the pro- gram in a file named  ):
):
yacas -pc sum.yacas 5050
Here the % symbol is the computer’s prompt. The result is 5,050, as expected. One way of stating this result is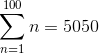
The capital Greek letter 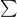 , sigma, is used because it makes the “s” sound, and that’s the first sound in the
word “sum.” The
, sigma, is used because it makes the “s” sound, and that’s the first sound in the
word “sum.” The  below the sigma says the sum starts at 1, and the
100 on top says it ends at 100. The
below the sigma says the sum starts at 1, and the
100 on top says it ends at 100. The  is what’s known as a dummy
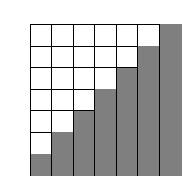
variable: it has no meaning outside the context of the sum. Figure 4.1 shows the graphical interpretation of the sum: we’re adding up the areas of a series of rectangular strips. (For clarity, the
figure only shows the sum going up to 7, rather than 100.)
is what’s known as a dummy
variable: it has no meaning outside the context of the sum. Figure 4.1 shows the graphical interpretation of the sum: we’re adding up the areas of a series of rectangular strips. (For clarity, the
figure only shows the sum going up to 7, rather than 100.)
Now how about an integral? Figure 4.2 shows the graphical interpretation of what we’re trying to do: find the area of the shaded triangle. This is an example we know how to do symbolically, so we
can do it numerically as well, and check the answers against each other. Symbolically, the area is given by the integral. To integrate the function 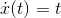 , we know we need some function with a
, we know we need some function with a 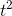 in it, since we want something whose derivative is
in it, since we want something whose derivative is 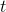 , and differentiation reduces the power by one. The derivative of
, and differentiation reduces the power by one. The derivative of 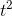 would be
would be 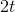 rather than
rather than 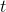 , so what
we want is
, so what
we want is 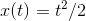 . Let’s compute the area of the triangle that
stretches along the
. Let’s compute the area of the triangle that
stretches along the  axis from 0 to 100:
axis from 0 to 100: 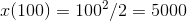 .
.
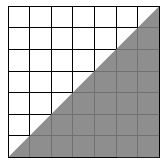
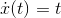
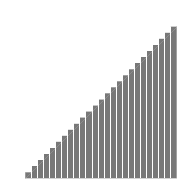
Figure 4.3 shows how to
accomplish the same thing numerically. We break up the area into a whole bunch of very skinny rectangles. Ideally, we’d like to make the width of each rectangle be an infinitesimal number
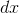 , so that we’d be adding up an infinite number of infinitesimal
areas. In reality, a computer can’t do that, so we divide up the interval from
, so that we’d be adding up an infinite number of infinitesimal
areas. In reality, a computer can’t do that, so we divide up the interval from 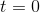 to
to 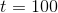 into
into 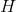 rectangles, each with finite width
rectangles, each with finite width 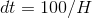 . Instead of making H
infinite, we make it the largest number we can without making the computer take too long to add up the areas of the rectangles.
. Instead of making H
infinite, we make it the largest number we can without making the computer take too long to add up the areas of the rectangles.
Example
tmax := 100; H := 1000; dt := tmax/H; sum := 0; t := 0; While (t<=tmax) [ sum := N(sum+t*dt); t := N(t+dt); ]; Echo(sum);
In Example, we split the interval from 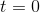 to 100 into
to 100 into 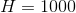 small intervals, each with width
small intervals, each with width 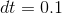 . The result is 5,005, which agrees with the symbolic result to three digits of precision. Changing
. The result is 5,005, which agrees with the symbolic result to three digits of precision. Changing 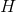 to 10,000 gives 5, 000.5, which is one more digit. Clearly as we make the number of
rectangles greater and greater, we're converging to the correct result of 5,000.
to 10,000 gives 5, 000.5, which is one more digit. Clearly as we make the number of
rectangles greater and greater, we're converging to the correct result of 5,000.
In the Leibniz notation, the thing we've just calculated, by two different techniques, is written like this:
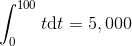 It looks a lot like the
It looks a lot like the  notation, with the
notation, with the  replaces by a flattened out letter “S.” The
replaces by a flattened out letter “S.” The  is a dummy variable. What I’ve been casually referring to as an integral is re- ally two
different but closely related things, known as the definite integral and the indefinite integral.
is a dummy variable. What I’ve been casually referring to as an integral is re- ally two
different but closely related things, known as the definite integral and the indefinite integral.
Definition of the indefinite integral
If 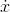 is a function, then a function
is a function, then a function 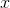 is an indefinite integral of
is an indefinite integral of 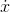 if, as implied by the notation,
if, as implied by the notation,
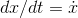 .
.
Interpretation: Doing an indefinite integral means doing the opposite of differentiation. All the possible indefinite integrals are the same function except for an additive constant.
Example
Find the indefinite integral of the function 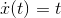 .
.
Any function of the form
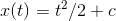
where  is a constant, is an indefinite integral of this function,
since its derivative is
is a constant, is an indefinite integral of this function,
since its derivative is 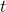 .
.
Definition of the definite integral
If 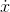 is a function, then the definite
integral of
is a function, then the definite
integral of 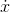 from a to b is defined as
from a to b is defined as
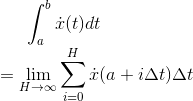
where 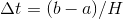
Interpretation: What we’re calculating is the area under the graph of 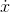 , from
, from  to
to 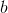 . (If the graph dips below the
. (If the graph dips below the 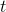 axis, we interpret the area between it and the axis as a negative area.) The thing inside the limit is a calculation like the
one done in Example, but generalized to
axis, we interpret the area between it and the axis as a negative area.) The thing inside the limit is a calculation like the
one done in Example, but generalized to 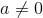 . If
. If 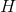 was infinite, then
was infinite, then 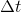 would be an infinitesimal number
would be an infinitesimal number 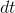 .
.
- 4548 reads






