Properties of the integral

Available under Creative Commons-ShareAlike 4.0 International License.

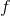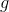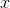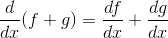
Let and be two functions of , and let be a constant. We already know that for derivatives, $\frac{d}{dx}(f+g)=\frac{df}{dx}+\frac{dg}{dx}$
and
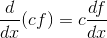
$\frac{d}{dx}(cf)=c\frac{df}{dx}$
But since the indefinite integral is just the operation of undoing a derivative, the same kind of rules must hold true for indefinite integrals as well:
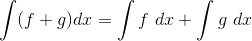$\int (f+g)dx=\int f\textrm{{ }}dx+\int g\textrm{{ }}dx$ and

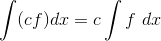
$\int (cf)dx=c\int f\textrm{{ }}dx$
And since a definite integral can be found by plugging in the upper and lower limits of integration into the indefinite integral, the same properties must be true of definite integrals as well.

Example

Evaluate the indefinite integral

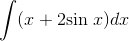$\int (x+2\textrm{sin }x)dx$ Using the additive property, the integral becomes

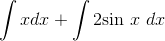
$\int xdx+\int 2\textrm{sin }x\textrm{{ }}dx$

Then the property of scaling by a constant lets us change this to

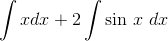
$\int xdx+2\int \textrm{sin }x\textrm{{ }}dx$

We need a function whose derivative is 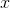, which would be 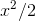x^2/2 , and one whose derivative is 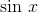$\textrm{sin }x$ , which must be 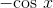$-\textrm{cos }x$ , so the result is

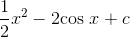
$\frac{1}{2}x^2-2\textrm{cos }x+c$

2299 reads

You are here

Properties of the integral

Example