Numerical method

Available under Creative Commons-ShareAlike 4.0 International License.

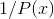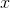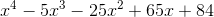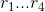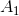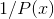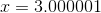Suppose we evaluate 1/P(x) for a value of very close to one of the roots. In the example of the polynomial x^4-5x^3-25x^2+65x+84 , let r_1...r_4 be the roots in the order in which they were re-turned by Yacas. Then A_1 can be found by evaluating 1/P(x) at x=3.000001 :

P(x):=x^4-5*x^3-25*x^2
 +65*x+84
N(1/P(3.000001))
 -8928.5702094768

We know that for 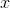very close to 3, the expression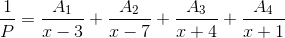 $\frac{1}{P}=\frac{A_1}{x-3}+\frac{A_2}{x-7}+\frac{A_3}{x+4}+\frac{A_4}{x+1}$

will be dominated by the 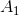A_1 term, so

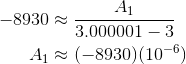
$\begin{align*} -8930&\approx\frac{A_1}{3.000001-3} \\ A_1&\approx(-8930)(10^{-6}) \end{align*}$

By the same method we can find the other four constants:

dx:=.000001
N(1/P(7+dx),30)*dx
 0.2840908276e-2
N(1/P(-4+dx),30)*dx
 -0.4329006192e-2
N(1/P(-1+dx),30)*dx
 0.1041666664e-1

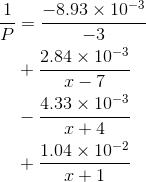
$\texttt{(The N( ,30)}$ construct is to tell Yacas to do a numerical calculation rather than an exact symbolic one, and to use 30 digits of precision, in order to avoid problems with rounding errors.) Thus, $\begin{align*} \frac{1}{P} &=\frac{-8.93\times 10^{-3}}{-3} \\ &+ \frac{2.84\times 10^{-3}}{x-7} \\ &- \frac{4.33\times 10^{-3}}{x+4} \\ &+ \frac{1.04\times 10^{-2}}{x+1} \end{align*}$

The desired integral is

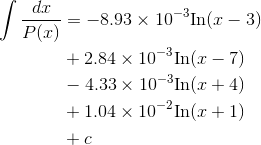
$\begin{align*} \int \frac{dx}{P(x)} &=-8.93\times 10^{-3}\textrm{In}(x-3) \\ &+2.84\times 10^{-3}\textrm{In}(x-7) \\ &-4.33\times 10^{-3} \textrm{In}(x+4) \\ &+ 1.04 \times 10^{-2}\textrm{In}(x+1) \\ &+ c \end{align*}$

As in the simpler example 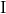$\textrm{I}$ started off with, where 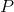was second or- der and we got 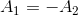A_1=-A_2 , in this 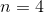n=4 example we expect that 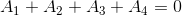A_1+A_2+A_3+A_4=0 , for otherwise the large- 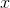behavior of the partial-fraction form would be 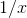1/x rather than 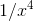1/x^4 . This is a useful way of checking the result: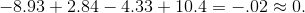 $-8.93+ 2.84 -4.33 + 10.4 = -.02 \approx 0.$

1440 reads

You are here

Numerical method