I told you not to worry about Safe use of infinitesimals. But since you’re reading this, you’re obviously in need of more reassurance.
For some of these functions, the transfer principle straightforwardly guarantees that they work for hyperreals, have all the familiar proper- ties, and can be computed in the same way. For
example, the following statement is in a suitable form to have the transfer principle applied to it: For any real
number x,x·x≥0.Changing “real” to “hyperreal,” we find out that the square of a hyperreal number is greater than
or equal to zero, just like the square of a real number. Writing it as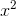 
or calling it a square is just a matter of notation and terminology. The same applies to this statement: For
any real number x≥0, there exists a real
number y such that 
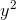= x. Applying the transfer function to it tells us that square roots can be defined for the hyperreals as well.
There’s a problem, however, when we get to functions like sin x and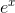 
. If you look up the definition of the sine function in a trigonometry textbook, it will be defined geometrically, as the ratio of
the lengths of two sides of a certain triangle. The transfer principle doesn’t apply to geometry, only to arithmetic. It’s not even obvious intuitively that it makes sense to define a sine
function on the hyperreals. In an application like the differentiation of the sine function on page 28, we only had to take sines of hyperreal numbers that were infinitesimally close to real
numbers, but if the sine is going to be a full-fledged function defined on the hyperreals, then we should be allowed, for example, to take the sine of an infinite number. What would that mean?
If you take the sine of a number like a million or a billion on your calculator, you just get some apparently random result between −1 and 1. The sine function wiggles back and forth
indefinitely as xgets bigger and bigger, never settling down to any specific limiting value. Apparently we could have sin H= 1 for a particular infinite H, and then
sin(H + π/2) = 0, sin(H + π) = −1,
. . .
It turns out that the moral equivalent of the transfer function can indeed be applied to any function on the reals, yielding a function that is in some sense its natural “big brother” on the the hyperreals, but the consequences can be either disturbing or exhilirating depending on your tastes. For example, consider the function [x] that takes a real number xand rounds it down to the greatest integer that is less than or equal to to x, e.g., [3] = 3, and [π] = 3. This function, like any other real function, can be extended to the hyperreals, and that means that we can define the hyperintegers, the set of hyperreals that satisfy [x] = x. The hyperintegers include the integers as a subset, but they also include infinite numbers. This is likely to seem magical, or even unreasonable, if we come at the hyperreals from a purely axiomatic point of view. The extension of functions to the hyperreals seems much more natural in view of the construction of the hyperreals in terms of sequences given in the preceding section. For example, the sequence 1.3, 2.3, 3.3, 4.3, 5.3, ...represents an infinite number. If we apply the [x] function to it, we get 1, 2, 3, 4, 5, ..., which is an infinite integer.
- 1133 reads
