All of the reasoning on page 39 would have applied equally well to any other exponential function with a different base, such as 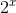 or
or 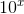 . Those functions would have different values of c, so if we want to deter- mine the value of cfor the
base-ecase, we need to bring in the definition of e, or of the exponential function
. Those functions would have different values of c, so if we want to deter- mine the value of cfor the
base-ecase, we need to bring in the definition of e, or of the exponential function 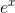 , somehow.
, somehow.
We can take the definition of 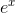 to be
to be
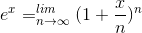
The idea behind this relation is similar to the idea of compound interest. If the interest rate is 10%, compounded annually, then x= 0.1, and the balance grows by a factor (1 +
x) = 1.1 in one year. If, instead, we want to compound the interest monthly, we can set the monthly interest rate to 0.1/12, and then the growth of the balance over a year is
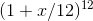 = 1.1047, which is slightly larger because the interest
from the earlier months itself accrues interest in the later months. Continuing this limiting process, we find
= 1.1047, which is slightly larger because the interest
from the earlier months itself accrues interest in the later months. Continuing this limiting process, we find 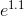 = 1.1052.
= 1.1052.
If n is large, then we have a good approximation to the base-e exponential, so let’s differentiate this finite-napproximation and try to find an approximation to the
derivative of 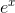 . The chain rule tells is that the derivative
of
. The chain rule tells is that the derivative
of 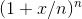 is the derivative of the raising-to-
the-nth-power function, multiplied by the derivative of the inside stuff,
is the derivative of the raising-to-
the-nth-power function, multiplied by the derivative of the inside stuff,
d(1 + x/n)/dx= 1/n. We then have
![\frac{d(1+\frac{x}{n})^{n}}{dx}=[n(1+\frac{x}{n})^{n-1}]\cdot \frac{1}{n}](/system/files/resource/33/33298/34193/media/eqn-img_10.gif)
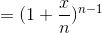
But evaluating this at x= 0 simply gives 1, so at x= 0, the approximation to the derivative is exactly 1 for all values of n— it’s not even necessary to imagine going to larger and larger values of n. This establishes that c= 1, so we have for all values of x.
- 2513 reads






