We start with the following lemma, which is intuitively obvious, because polynomials don’t have asymptotes. Its proof is given after the proof of the main theorem.
Lemma: For any polynomial P(z) in the complex plane, its magnitude |P(z)| achieves its minimum value at some specific point 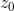 .
.
The fundamental theorem of algebra: In the complex number system, a nonzero nth-order polynomial has exactly nroots, i.e., it can be factored into the form P(z) =
(z−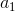 )(z−
)(z− 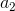 ) ...(z−
) ...(z− 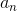 ), where the ai are complex numbers.
), where the ai are complex numbers.
Proof: The proofs in the cases of n= 0 and 1 are trivial, so our strategy is to reduce higher-ncases to lower ones. If an nth-degree polynomial P has at least one root, a, then we can always reduce it to a polynomial of degree n−1 by dividing it by (z−a). Therefore the theorem is proved by induction provided that we can show that every polynomial of degree greater than zero has at least one root.
Suppose, on the contrary, that there is an nth order polynomial P(z), with n>0, that has no roots at all. Then by the lemma |P|
achieves its minimum value at some point 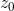 . To make things more
simple and concrete, we can construct another polynomial Q(z) = P(z+
. To make things more
simple and concrete, we can construct another polynomial Q(z) = P(z+ 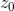 )/P(
)/P(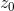 ), so that |Q| has a minimum value of 1, achieved at Q(0) = 1. This means that Q’s
constant term is 1. What about its other terms? Let Q(z) = 1+
), so that |Q| has a minimum value of 1, achieved at Q(0) = 1. This means that Q’s
constant term is 1. What about its other terms? Let Q(z) = 1+ 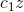 + ...+
+ ...+ 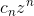 . Suppose
. Suppose 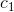 was nonzero. Then for infinitesimally small values of z, the terms of order z2 and higher would be negligible,
and we could make Q(z) be a real number less than one by an appropriate choice of z’s argument. Therefore c1 must be zero. But that means that if
was nonzero. Then for infinitesimally small values of z, the terms of order z2 and higher would be negligible,
and we could make Q(z) be a real number less than one by an appropriate choice of z’s argument. Therefore c1 must be zero. But that means that if 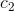 is nonzero, then for infinitesimally small z, the
is nonzero, then for infinitesimally small z, the 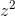 term dominates the
term dominates the 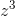 and higher terms, and again this would allow us to make Q(z) be real
and less than one for appropriately chosen values of z. Continuing this process, we find that Q(z) has no terms at all beyond the constant term, i.e.,
Q(z) = 1. This contradicts the assumption that nwas greater than zero, so we’ve proved by contradiction that there is no P with the properties claimed.
and higher terms, and again this would allow us to make Q(z) be real
and less than one for appropriately chosen values of z. Continuing this process, we find that Q(z) has no terms at all beyond the constant term, i.e.,
Q(z) = 1. This contradicts the assumption that nwas greater than zero, so we’ve proved by contradiction that there is no P with the properties claimed.
Uninteresting proof of the lemma: Let M(r) be the minimum value of |P(z)|on the disk defined by |z|≤r. We first prove that M(r) can’t asymptotically approach a minimum as rapproaches infinity. Suppose to the contrary: for every r, there is some r'>rwith M(r') <M(r).
Then by the transfer principle, the same would have to be true for hyperreal values of r. But it’s clear that if ris infinite, the lower-order terms of Pwill be infinitesimally small compared to the highest-order term, and therefore M(r) is infinite for infinite values of r, which is a contradiction, since by construction M is decreasing, and finite for finite r. We can therefore conclude by the extreme value theorem that M achieves its minimum for some specific value of r. The least such rdescribes a circle |z|= rin the complex plane, and the minimum of |P|on this circle must be the same as its global minimum. Applying the extreme value function to |P(z)|as a function of arg zon the interval 0 ≤argz≤2π, we establish the desired result.
- 2611 reads






