Available under Creative Commons-ShareAlike 4.0 International License.
The plane of Euclidean geometry is today often described as the set of all coordinate pairs 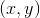 , where
, where 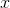 and
and 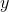 are real. We could instead imagine the plane F that is defined in the same way, but with
are real. We could instead imagine the plane F that is defined in the same way, but with 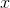 and
and 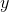 taken from the
set of hyperreal numbers. As a third alternative, there is the plane G in which the finite hyperreals are used. In E, Euclid's parallel postulate holds: given a line and a point not on the
line, there exists exactly one line passing through the point that does not intersect the line. Does the parallel postulate hold in F? In G? Is it valid to associate only E with the plane
described by Euclid's axioms? .
taken from the
set of hyperreal numbers. As a third alternative, there is the plane G in which the finite hyperreals are used. In E, Euclid's parallel postulate holds: given a line and a point not on the
line, there exists exactly one line passing through the point that does not intersect the line. Does the parallel postulate hold in F? In G? Is it valid to associate only E with the plane
described by Euclid's axioms? .
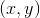 , where
, where 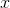 and
and 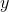 are real. We could instead imagine the plane F that is defined in the same way, but with
are real. We could instead imagine the plane F that is defined in the same way, but with 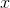 and
and 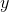 taken from the
set of hyperreal numbers. As a third alternative, there is the plane G in which the finite hyperreals are used. In E, Euclid's parallel postulate holds: given a line and a point not on the
line, there exists exactly one line passing through the point that does not intersect the line. Does the parallel postulate hold in F? In G? Is it valid to associate only E with the plane
described by Euclid's axioms? .
taken from the
set of hyperreal numbers. As a third alternative, there is the plane G in which the finite hyperreals are used. In E, Euclid's parallel postulate holds: given a line and a point not on the
line, there exists exactly one line passing through the point that does not intersect the line. Does the parallel postulate hold in F? In G? Is it valid to associate only E with the plane
described by Euclid's axioms? .
- 2558 reads






