Euler was the first to prove 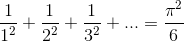 This problem had defeated other great mathematicians of his time, and was famous enough to be given a special name, the Basel
problem. Here we present an argument based closely on Euler’s and pose the problem of how to exploit Euler’s technique further in order to prove
This problem had defeated other great mathematicians of his time, and was famous enough to be given a special name, the Basel
problem. Here we present an argument based closely on Euler’s and pose the problem of how to exploit Euler’s technique further in order to prove 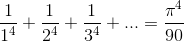 From the Taylor
series for the sine function, we nd the related series
From the Taylor
series for the sine function, we nd the related series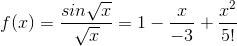 The partial sums of this series are polynomials that approximate f for small values of x. If such a polynomial were exact rather
than approximate, then it would have zeroes at x =
The partial sums of this series are polynomials that approximate f for small values of x. If such a polynomial were exact rather
than approximate, then it would have zeroes at x = 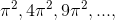 , and we could write it as the product of its linear factors. Euler assumed, without any more rigorous proof, that this
factorization procedure could be extended to the in nite series, so that f could be represented as the in nite product
, and we could write it as the product of its linear factors. Euler assumed, without any more rigorous proof, that this
factorization procedure could be extended to the in nite series, so that f could be represented as the in nite product 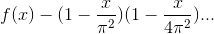 By multiplying this out and equating its linear term to that of the Taylor series, we nd the claimed
result. Extend this procedure to the
By multiplying this out and equating its linear term to that of the Taylor series, we nd the claimed
result. Extend this procedure to the 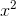 term and prove the
result claimed for the sum of the inverse fourth powers of the integers. (The sums with odd exponents 3 are much harder, and relatively little is known about them. The sum of the inverse cubes
is known as Apery's constant.)
term and prove the
result claimed for the sum of the inverse fourth powers of the integers. (The sums with odd exponents 3 are much harder, and relatively little is known about them. The sum of the inverse cubes
is known as Apery's constant.)
- 1703 reads






