Available under Creative Commons-ShareAlike 4.0 International License.
To which of the following statements can the transfer principle be applied? If you think it can't be applied to a certain statement, try to prove that the statement is false for the hyperreals, e.g., by giving a counterexample.
- For any real numbers
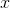 and
and 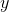 ,
, 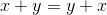 .
.
- The sine of any real number is between -1 and 1.
- For any real number
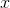 , there exists another real number
, there exists another real number 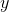 that is greater than
that is greater than 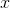 .
.
- For any real numbers
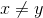 , there exists
another real number
, there exists
another real number  such that
such that 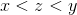 .
.
- For any real numbers
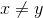 , there exists a rational number
, there exists a rational number  such that
such that 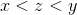 . (A rational number is
one that can be expressed as an integer divided by another integer.)
. (A rational number is
one that can be expressed as an integer divided by another integer.)
- For any real numbers
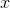 ,
, 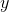 , and
, and  ,
, 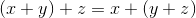 .
.
- For any real numbers
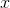 and
and 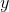 , either
, either 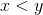 or
or 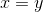 or
or 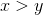
- For any real number
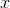 ,
, 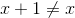 .
.
- 2127 reads






