Available under Creative Commons-ShareAlike 4.0 International License.
Consider the equationf'(x) = f(f(x)). This is known as a differential equation: an equation that relates a function to its own derivatives.
What is unusual about this differential equation is that the right-hand side involves the function nested inside itself. Given, for example, the value of f(0), we expect the solution
of this equation to exist and to be uniquely defined for all values of x. That doesn’t mean, however, that we can write down such a solution as a closed-form expression. Show that two
closed-form expressions do exist, of the form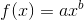
, and
find the two values of b.
- 2110 reads
