Problems like this come up frequently. Imagine that each household in a certain small town sends a total of one ton of garbage to the dump every year. Over time, the garbage accumulates in the dump, taking up more and more space.

Let's label the years as 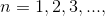 and let the function
1
and let the function
1 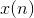 represent the amount of garbage that has accumulated by the end of year
represent the amount of garbage that has accumulated by the end of year 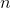 . If the population is constant, say 13 households, then garbage accumulates at a
constant rate, and we have
. If the population is constant, say 13 households, then garbage accumulates at a
constant rate, and we have 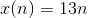 .
.
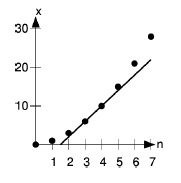
But maybe the town's population is growing. If the population starts out as 1 household in year 1, and then grows to 2 in year 2, and soon, then we have the same kind of problem that the young
Gauss solved. After 100 years, the accumulated amount of garbage will be 5,050 tons. The pile of refuse grows more quickly every year; the rate of change of 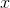 is not constant. Tabulating the examples we've done so far, we have this:
is not constant. Tabulating the examples we've done so far, we have this:
|
rate of change |
Accumulated result |
| 13 |
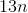
|
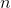
|
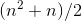
|
The rate of change of the function 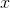 can be notated as
can be notated as 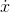 . Given the function
. Given the function 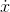 , we
can always determine the function
, we
can always determine the function 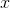 for any value of
for any value of 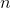 by doing a running sum.
by doing a running sum.
Likewise, if we know 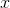 , we can determine
, we can determine 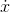 by subtraction. In the example where
by subtraction. In the example where 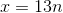 , we can find
, we can find 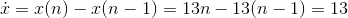 . Or if we knew that the accumulated amount of garbage was given by
. Or if we knew that the accumulated amount of garbage was given by 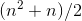 , we could calculate the town's population like this:
, we could calculate the town's population like this:
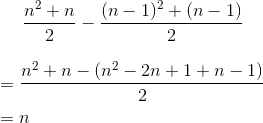
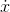 is the slope of x.
is the slope of x.
The graphical interpretation of this is shown in Figure 1.4: on a graph of
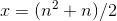 , the slope of the line connecting two successive points is
the value of the function
, the slope of the line connecting two successive points is
the value of the function 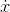 .
.
In other words, the functions 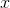 and
and 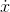 are like different sides of the same coin. If you know one, you can find the other |
with two caveats.
are like different sides of the same coin. If you know one, you can find the other |
with two caveats.
First, we've been assuming implicitly that the function 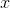 starts out at
starts out at
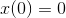 . That might not be true in general. For instance, if we're
adding water to a reservoir over a certain period of time, the reservoir probably didn't start out completely empty. Thus, if we know
. That might not be true in general. For instance, if we're
adding water to a reservoir over a certain period of time, the reservoir probably didn't start out completely empty. Thus, if we know 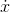 , we can't find out everything about
, we can't find out everything about 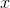 without some further information: the starting value of
without some further information: the starting value of 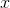 . If someone tells you
. If someone tells you 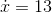 , you can't conclude
, you can't conclude 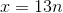 , but only
, but only 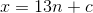 , where
, where  is some constant. There's no such ambiguity if you're going the opposite way, from
is some constant. There's no such ambiguity if you're going the opposite way, from 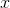 to
to 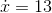 .
Even if
.
Even if 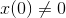 , we still have
, we still have ![\dot{x}=13n+c-[13(n-1)+c]=13](/system/files/resource/33/33298/33301/media/eqn-img_37.gif) .
.
Second, it may be difficult, or even impossible, to find a formula for the answer when we want to determine the running sum 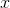 given
a formula for the rate of change
given
a formula for the rate of change  . Gauss had a flash of insight that led him to the result
. Gauss had a flash of insight that led him to the result 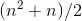 , but in general we might only be able to use a computer spreadsheet to
calculate a number for the running sum, rather than an equation that would be valid for all values of
, but in general we might only be able to use a computer spreadsheet to
calculate a number for the running sum, rather than an equation that would be valid for all values of 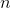 .
.
- 2529 reads






