Even though we lack Gauss's genius, we can recognize certain patterns. One pattern is that if 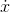 is a function that gets bigger and bigger, it seems like
is a function that gets bigger and bigger, it seems like 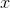 will be a function that grows even faster than
will be a function that grows even faster than 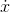 . In
the example of
. In
the example of 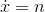 and
and 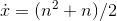 , consider what happens for a large value of n, like 100. At this value of
, consider what happens for a large value of n, like 100. At this value of 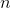 ,
, 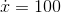 , which is pretty big, but even without pawing around for a calculator, we know that
, which is pretty big, but even without pawing around for a calculator, we know that 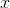 is going to turn out really really big. Since
is going to turn out really really big. Since 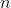 is large,
is large, 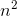 is quite a bit bigger than
is quite a bit bigger than 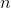 , so
roughly speaking, we can approximate
, so
roughly speaking, we can approximate 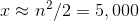 . 100 may be a
big number, but 5,000 is a lot bigger. Continuing in this way, for
. 100 may be a
big number, but 5,000 is a lot bigger. Continuing in this way, for 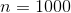 we have
we have 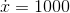 , but
, but  --- now
--- now 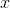 has far outstripped
has far outstripped 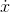 . This can be a fun game to play with a calculator: look at which
functions grow the fastest. For instance, your calculator might have an
. This can be a fun game to play with a calculator: look at which
functions grow the fastest. For instance, your calculator might have an 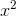 button, an
button, an 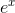 button, and a button for
button, and a button for 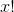 (the factorial function, defined as
(the factorial function, defined as 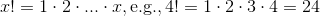 ). You'll find that
). You'll find that 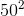 is pretty big, but
is pretty big, but 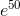 is incomparably greater, and
is incomparably greater, and 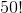 Is so big that it causes an error.
Is so big that it causes an error.
All the 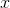 and
and 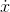 functions we've seen so far have been polynomials. If
functions we've seen so far have been polynomials. If 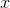 is a polynomial, then of course we can find a polynomial for
is a polynomial, then of course we can find a polynomial for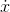 as well, because if
as well, because if 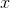 is a polynomial, then
is a polynomial, then 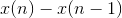 will be one too. It also looks like every polynomial we could choose for
will be one too. It also looks like every polynomial we could choose for 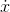 might also correspond to an
might also correspond to an 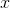 that's a polynomial. And not only that, but it looks as though there's a
pattern in the power of
that's a polynomial. And not only that, but it looks as though there's a
pattern in the power of 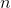 . Suppose
. Suppose 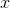 is a polynomial, and the highest power of
is a polynomial, and the highest power of 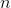 it contains is a certain number - the “order” of the polynomial. Then
it contains is a certain number - the “order” of the polynomial. Then
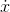 is a polynomial of that order minus one. Again, it's fairly easy to
prove this going one way, passing from
is a polynomial of that order minus one. Again, it's fairly easy to
prove this going one way, passing from 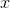 to
to 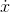 ,
but more difficult to prove the opposite relationship: that if
,
but more difficult to prove the opposite relationship: that if 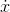 is a polynomial of a certain order, then
is a polynomial of a certain order, then 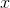 must be a polynomial with an order that's greater by one.
must be a polynomial with an order that's greater by one.
We'd imagine, then, that the running sum of 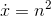 would be a
polynomial of order 3. If we calculate
would be a
polynomial of order 3. If we calculate 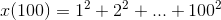 on a
computer spreadsheet, we get 338,350, which looks suspiciously close to 1,000,000/3. It looks like
on a
computer spreadsheet, we get 338,350, which looks suspiciously close to 1,000,000/3. It looks like 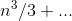 , where the dots represent terms involving lower powers of
, where the dots represent terms involving lower powers of 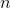 such as
such as 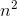 . The fact that the coefficient of the
. The fact that the coefficient of the 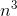 term is 1/3 is proved in Problem 1.21.
term is 1/3 is proved in Problem 1.21.
Example
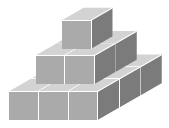
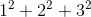
Figure 1.5 shows a pyramid consisting of a
single cubical block on top, supported by a 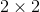 layer,
supported in turn by a
layer,
supported in turn by a 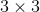 layer. The total volume is
layer. The total volume is 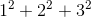 , in units of the volume of a single block.
, in units of the volume of a single block.
Generalizing to the sum 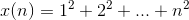 ,and applying the result
of the preceding paragraph, we find that the volume of such a pyramid is approximately
,and applying the result
of the preceding paragraph, we find that the volume of such a pyramid is approximately 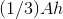 , where
, where 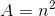 is the area of the base and
is the area of the base and 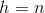 is the height.
is the height.
When 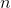 is very large, we can get as good an approximation as we like
to a smooth-sided pyramid, and the error incurred in
is very large, we can get as good an approximation as we like
to a smooth-sided pyramid, and the error incurred in 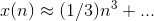 by omitting the lower-order terms ... can be made as small as desired.
by omitting the lower-order terms ... can be made as small as desired.
We therefore conclude that the volume is exactly 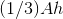 for a smooth sided pyramid
with these proportions.
for a smooth sided pyramid
with these proportions.
This is a special case of a theorem first proved by Euclid (propositions XII-6 and XII-7) two thousand years before calculus was invented.
- 3321 reads






