The Women's National Basketball Association says that balls used in its games should have a radius of 11.6 cm, with an allowable range of error of plus or minus 0.1 cm (one millimeter). How accurately can we determine the ball's volume?
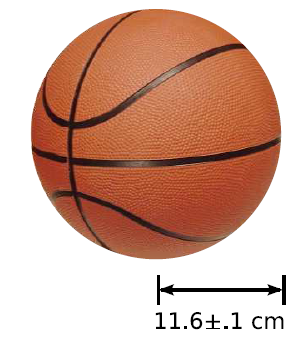
The equation for the volume of a sphere gives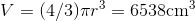 
(about six and a half liters). We have a function 
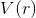, and we want to know how much of an effect will be produced on the function's output 
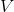if its input 
is changed by a certain small amount. Since the amount by which 
can be
changed is small compared to 
, it's reasonable to take the tangent line as an approximation to the
actual graph. The slope of the tangent line is the derivative of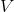 
, which is 
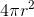. (This is the ball's surface area.) Setting (slope) = (rise)/(run) and solving for the
rise, which represents the change in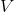 
, we find that it could be off by as much as 
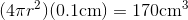. The volume of the ball can
therefore be expressed as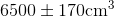 
, where the original
figure of 6538 has been rounded off to the nearest hundred in order to avoid creating the impression that the 3 and the 8 actually mean anything | they clearly don't, since the possible error
is out in the hundreds' place.
This calculation is an example of a very common situation that occurs in the sciences, and even in everyday life, in which we base a calculation on a number that has some range of uncertainty in it, causing a corresponding range of uncertainty in the _nal result. This is called propagation of errors. The idea is that the derivative expresses how sensitive the function's output is to its input.
The example of the basketball could also have been handled without calculus, simply by recalculating the volume using a radius that was raised from 11.6 to 11.7 cm, and finding the difference between the two volumes. Understanding it in terms of calculus, however, gives us a different way of getting at the same ideas, and often allows us to understand more deeply what's going on. For example, we noticed in passing that the derivative of the volume was simply the surface area of the ball, which provides a nice geometric visualization. We can imagine inflating the ball so that its radius is increased by a millimeter. The amount of added volume equals the surface area of the ball multiplied by one millimeter, just as the amount of volume added to the world's oceans by global warming equals the oceans' surface area multiplied by the added depth.
For an example of an insight that we would have missed if we hadn't applied calculus, consider how much error is incurred in the measurement of the width of a book if the ruler is placed on the book at a slightly incorrect angle, so that it doesn't form an angle of exactly 90 degrees with spine. The measurement has its minimum (and correct) value if the ruler is placed at exactly 90 degrees. Since the function has a minimum at this angle, its derivative is zero. That means that we expect essentially no error in the measurement if the ruler's angle is just a tiny bit o_. This gives us the insight that it's not worth fiddling excessively over the angle in this measurement. Other sources of error will be more important. For example, is the book a uniform rectangle? Are we using the worn end of the ruler as its zero, rather than letting the ruler hang over both sides of the book and subtracting the two measurements?
- 1219 reads
