When a function goes up and then smoothly turns around and comes back down again, it has zero slope at the top. A place where 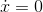 , then, could represent a place where
, then, could represent a place where 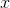 was at a maximum. On the other hand, it could be concave up, in which case we'd have a minimum. The term extremum refers to either
a maximum or a minimum.
was at a maximum. On the other hand, it could be concave up, in which case we'd have a minimum. The term extremum refers to either
a maximum or a minimum.
Example
Fred receives a mysterious e-mail tip telling him that his investment in a certain stock will have a value given by 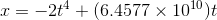 , where
, where 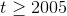 is the year. Should he sell at some point? If so, when?
is the year. Should he sell at some point? If so, when?
If the value reaches a maximum at some time, then the derivative should be zero then. Taking the derivative and setting it equal to zero, we have
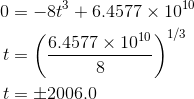
Obviously the solution at 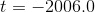 is bogus, since the stock market
didn’t exist four thousand years ago, and the tip only claimed the function would be valid for
is bogus, since the stock market
didn’t exist four thousand years ago, and the tip only claimed the function would be valid for 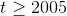 .
.
Should Fred sell on New Year’s eve of 2006?
But this could be a maximum, a minimum, or an inflection point. Fred definitely does not want to sell at 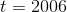 if it’s a minimum! To check which of the three possibilities hold, Fred takes the second derivative:
if it’s a minimum! To check which of the three possibilities hold, Fred takes the second derivative:
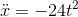
Plugging in 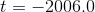 , we find that the second
derivative is negative at that time, so it is indeed a maximum.
, we find that the second
derivative is negative at that time, so it is indeed a maximum.
Implicit in this whole discussion was the assumption that the maximum or minimum occurred where the function was smooth. There are some other possibilities.
In Figure 1.14, the function's minimum occurs at an end-point of its domain.
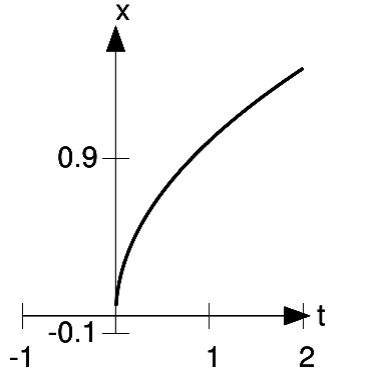
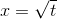 has a minimum at
has a minimum at 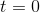 , which is not a place where
, which is not a place where 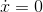 . This point is the edge of the function’s domain.
. This point is the edge of the function’s domain.
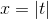 has a minimum at
has a minimum at 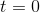 , which is not a place where
, which is not a place where 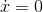 . This is a point where the function isn’t differentiable.
. This is a point where the function isn’t differentiable.
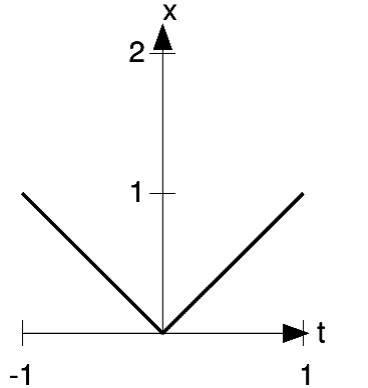
Another possibility is that the function can have a minimum or maximum at some point where its derivative isn't well defined. Figure 1.15 shows such a situation. There is a kink in the function at 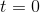 , so a wide variety of lines could be placed through the graph there, all with different
slopes and all staying on one side of the graph. There is no uniquely defined tangent line, so the derivative is undefined.
, so a wide variety of lines could be placed through the graph there, all with different
slopes and all staying on one side of the graph. There is no uniquely defined tangent line, so the derivative is undefined.
Example
Rancher Rick has a length of cyclone fence  with which to enclose a rectangular pasture. Show that he can enclose the
greatest possible area by forming a square with sides of length
with which to enclose a rectangular pasture. Show that he can enclose the
greatest possible area by forming a square with sides of length 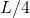 .
.
If the width and length of the rectangle are 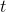 and
and
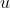 , and Rick is going
to use up all his fencing material, then the perimeter of the rectangle,
, and Rick is going
to use up all his fencing material, then the perimeter of the rectangle, 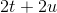 , equals
, equals 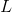 , so for a given width,
, so for a given width, 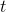 , the length is
, the length is 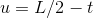 . The area is
. The area is 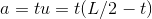 . The function only means anything realistic for
. The function only means anything realistic for 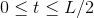 , since for values
of
, since for values
of 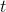 outside this
region either the width or the height of the rectangle would be negative. The function
outside this
region either the width or the height of the rectangle would be negative. The function 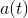 could therefore have a maximum either at a place where
could therefore have a maximum either at a place where 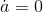 , or at the
endpoints of the function’s domain. We can eliminate the latter possibility, because the areais zero at the endpoints.
, or at the
endpoints of the function’s domain. We can eliminate the latter possibility, because the areais zero at the endpoints.
To evaluate the derivative, we first need to reexpress a as a polynomial
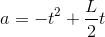
The derivative is
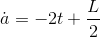
Setting this equal to zero, we find
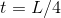 , as claimed. This is a
maximum, not a minimum or an inflection point, because the second derivative is the constant
, as claimed. This is a
maximum, not a minimum or an inflection point, because the second derivative is the constant 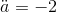 , which is negative for all
, which is negative for all 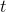 , including
, including 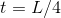 .
.- 4451 reads






