In Partial fractions I introduced the trick of carrying
out the method of partial fractions by evaluating 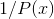 numerically at
numerically at
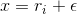 , near where
, near where 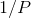 blows up. Sometimes we would like to have an exact result rather than a numerical
approximation. We can accomplish this by using an infinitesimal number dx rather than a small but finite
blows up. Sometimes we would like to have an exact result rather than a numerical
approximation. We can accomplish this by using an infinitesimal number dx rather than a small but finite  . For simplicity, let's assume that all of the
. For simplicity, let's assume that all of the 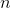 roots
roots 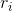 are distinct, and that
are distinct, and that 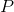 's highest-order term is
's highest-order term is 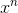 . We can then write
. We can then write 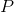 as the
product
as the
product 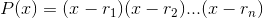 . For products like this, there is
a notation
. For products like this, there is
a notation 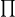 (capital Greek letter "pi") that works like
(capital Greek letter "pi") that works like 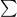 does for sums:
does for sums:
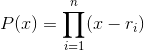
It’s not necessary that the roots be real, but for now we assume that they are. We want to find the coefficients 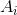 such that
such that 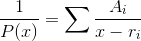
We then have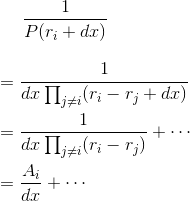
where … represents finite terms that are negligible compared to the infinite ones. Multiplying on both sides by 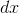 , we have
, we have
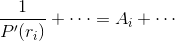
where the … now stand for infinitesimals which must in fact cancel out, since both 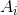 i and
i and 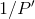 are real numbers.
are real numbers.
Example
The partial-fraction decomposition of the function
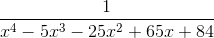 was found numerically
on Partial fractions. The coefficient of the
was found numerically
on Partial fractions. The coefficient of the 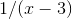 term was found numerically to be
term was found numerically to be 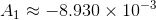 . Determine it exactly using the residue
method.
. Determine it exactly using the residue
method.
Differentiation gives 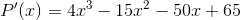 . We then have
. We then have 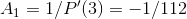 .
.
- 2809 reads






