Integral calculus was invented in the age of powdered wigs and harpsichords, so the original emphasis was on expressing integrals in a form that would allow numbers to be plugged in for easy numerical evaluation by scribbling on scraps of parchment with a quill pen. This was an era when you might have to travel to a large city to get access to a table of logarithms.
In this computationally impoverished environment, one always wanted to get answers in what’s known as closed form and in terms of elementary functions.
A closed form expression means one written using a finite number of operations, as opposed to something like the geometric series 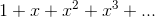 , which goes on forever.
, which goes on forever.
Elementary functions are usually taken to be addition, subtraction, multiplication, division, logs, and exponentials, as well as other functions derivable from these. For ex- ample, a cube root
is allowed, since 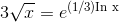 , and so are trig
functions and their inverses, since, as we will see in chapter 8, they can be expressed in terms of logs and exponentials.
, and so are trig
functions and their inverses, since, as we will see in chapter 8, they can be expressed in terms of logs and exponentials.
In theory, “closed form” doesn’t mean anything unless we state the elementary functions that are al- lowed. In practice, when people refer to closed form, they usually have in mind the particular set of elementary functions described above.
A traditional freshman calculus course spends such a vast amount of time teaching you how to do integrals in closed form that it may be easy to miss the fact that this is impossible for the
vast majority of integrands that you might randomly write down. Here are some examples of impossible integrals: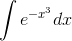
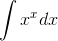
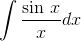
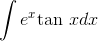
The first of these is a form that is extremely important in statistics (it describes the area under the standard "bell curve"), so you can see that impossible integrals aren't just obscure things that don't pop up in real life.
People who are proficient at doing integrals in closed form generally seem to work by a process of pat- tern matching. They recognize certain integrals as being of a form that can’t be done, so they know not to try.
Example
Students! Stand at attention! You will now evaluate 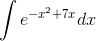 in closed form.
in closed form.
No sir, I can’t do that. By a change of variables of the form
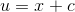 , where
, where  is a constant, we could clearly put this into the form
is a constant, we could clearly put this into the form 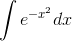 know is impossible.
know is impossible.
Sometimes an integral such as 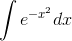 is important enough that
we want to give it a name, tabulate it, and write computer subroutines that can evaluate it numerically. For example, statisticians define the “error function”
is important enough that
we want to give it a name, tabulate it, and write computer subroutines that can evaluate it numerically. For example, statisticians define the “error function” 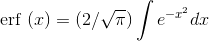 Sometimes if you're not sure whether an integral can be done in closed form, you
can put it into computer software, which will tell you that it reduces to one of these functions. You then know that it can't be done in closed form. For example, if you ask the popular web
site integrals.com to do
Sometimes if you're not sure whether an integral can be done in closed form, you
can put it into computer software, which will tell you that it reduces to one of these functions. You then know that it can't be done in closed form. For example, if you ask the popular web
site integrals.com to do 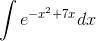 , it spits back
, it spits back 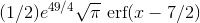 . This tells you both that you
shouldn't be wasting your time trying to do the integral in closed form and that if you need to evaluate it numerically, you can do that using the erf function.
. This tells you both that you
shouldn't be wasting your time trying to do the integral in closed form and that if you need to evaluate it numerically, you can do that using the erf function.
As shown in the following example, just because an indefinite integral can’t be done, that doesn’t mean that we can never do a related definite integral.
Example
Evaluate 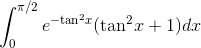 .
.
The obvious substitution to try is 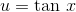 , and this
reduces the integrand to
, and this
reduces the integrand to 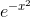 . This proves that the corre-
sponding indefinite integral is impossible to express in closed form. How- ever, the definite integral can be expressed in closed form; it turns out to be
. This proves that the corre-
sponding indefinite integral is impossible to express in closed form. How- ever, the definite integral can be expressed in closed form; it turns out to be 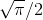 . The trick for proving this is given in Example 99.
. The trick for proving this is given in Example 99.
Sometimes computer software can’t say anything about a particular integral at all. That doesn’t mean that the integral can’t be done. Computers are stupid, and they may try brute-force
techniques that fail because the computer runs out of memory or CPU time For example, the integral 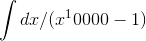 (Problem
8.5) can be done in closed form using the techniques of chapter 8, and it’s not too hard for a proficient human to figure out how to attack it, but every computer program I’ve tried it on
has failed silently.
(Problem
8.5) can be done in closed form using the techniques of chapter 8, and it’s not too hard for a proficient human to figure out how to attack it, but every computer program I’ve tried it on
has failed silently.
- 5390 reads






