Given a function x(t), consider any point P = (a, x(a)) on its graph. Let the function`(t) be a line passing through P. We say that `cuts through xat P if there exists some real number d>0 such that the graph of `is on one side of the graph of xfor all a−d<t<a, and is on the other side for all a<t<a+ d.
Definition (Marsden 1 ): A line `through P is said to be the line tangent to xat P if all lines through P with slopes less than that of ` cut through xin one direction, while all lines with slopes greater than P’s cut through it in the opposite direction.
The reason for the complication in the definition is that there are cases in which the function is smooth and well-behaved throughout a certain region, but for a certain point P in that region,
all lines through P cut through P. For example, the function x(t) = 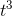 is blessed everywhere with lines that don’t cut through it — everywhere, that is, except at t= 0, which is an
inflection point (p. 17). Our definition fills in the “gap tooth” in the derivative function in the obvious way.
is blessed everywhere with lines that don’t cut through it — everywhere, that is, except at t= 0, which is an
inflection point (p. 17). Our definition fills in the “gap tooth” in the derivative function in the obvious way.
Example 103
As an example, we demonstrate that the derivative of 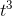 is zero
where it passes through the origin. Define the line `(t) = btwith slope b, passing through the origin. For b<0,
`cuts the graph of
is zero
where it passes through the origin. Define the line `(t) = btwith slope b, passing through the origin. For b<0,
`cuts the graph of 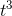 once at the origin, going down and
to the right. For b>0, `cuts the graph of
once at the origin, going down and
to the right. For b>0, `cuts the graph of 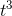 in three places, at t= 0 and ±√b.
in three places, at t= 0 and ±√b.
Picking any positive value of dless than √b, we find that `cuts the graph at the origin, going up and to the right. Therefore b= 0 gives the tangent line at the origin.
- 2932 reads






