Some ideas in this proof are due to Tom Goodwillie. Theorem: For n= 0, 1, 2, . . . ,the derivative of the function xdefined by x(t) = 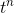 is x˙ =
is x˙ = 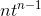 .
.
The results for n= 0 and 1 hold by direct application of the definition of the derivative.
For n>1, it suffices to prove  (0) = 0 and
(0) = 0 and
 (1) = n, since the result for other nonzero values of
tthen follows by the kind of scaling argument used on page 13 for the n= 2 case.
(1) = n, since the result for other nonzero values of
tthen follows by the kind of scaling argument used on page 13 for the n= 2 case.
We use the following properties of the derivative, all of which follow immediately from its definition as the slope of the tangent line:
Shift. Shifting a function x(t) horizontally to form a new function x(t+c) gives a derivative at any newly shifted point that is the same as the derivative at the corresponding point on the unshifted graph.
Flip. Flipping the function x(t) to form a new function x(−t) negates its derivative at t= 0.
Add. The derivative of the sum or difference of two functions is the sum or difference of their derivatives.
For even n, 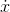 (0) = 0 follows from the flip property,
since x(−t) is the same function as x(t). For n= 3, 5, . . . , we apply the definition of the derivative in the same manner as was done in
the preceding section for
(0) = 0 follows from the flip property,
since x(−t) is the same function as x(t). For n= 3, 5, . . . , we apply the definition of the derivative in the same manner as was done in
the preceding section for
n= 3.
We now need to show that 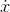 (1) = n. Define the function
uas
(1) = n. Define the function
uas
u(t) = x(t+ 1) −x(t)
= 1 + nt+ ... ,
where the second line follows from the binomial theorem, and. . . represents terms involving 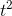 and higher powers. Since we’ve already established the results for n= 0 and 1, differentiation gives
and higher powers. Since we’ve already established the results for n= 0 and 1, differentiation gives
u˙ (t) = n+ ... .
Now let’s evaluate this at t= 0, where, as shown earlier, the terms represented by . . . all vanish. Applying the add and shift properties, we have
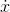 (1) −
(1) − 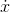 (0) = n .
(0) = n .
But since 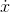 (0) = 0, this completes the proof.
(0) = 0, this completes the proof.
Although this proof was for integer exponents n≥1, the result is also true for any real value of n; see example 24 on p. 41.
- 2539 reads






