There are three parts to the proof: (1) Take the equation that states the fundamental theorem, differentiate both sides with respect to b, and show that they’re equal. (2) Show that continuous functions with equal derivatives must be essentially the same function, except for an additive constant. (3) Show that the constant in question is zero.
1. By the definition of the indefinite integral, the derivative of x(b)−x(a) with respect to bequals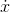 
(b). We have to establish that this equals the following:
![\begin{align*} \frac{d}{db}\int_{a}^{b}\dot{x}(t)dt&=st\frac{1}{db}\left [ \int_{a}^{b+db}\dot{x} (t)dt-\int_{a}^{b}\dot{x}(t)dt\right ] \\&=st\frac{1}{db} \int_{b}^{b+db}\dot{x} (t)dt \\&=st\frac{1}{db} _{H\rightarrow \infty }^{lim}\sum_{i=o}^{H}\dot{x}(b+idb/H)\frac{db}{H} \\&=st _{H\rightarrow \infty}^{lim}\frac{1}{H}^{lim}\sum_{i=o}^{H}\dot{x}(b+idb/H)\end{align*}](/system/files/resource/33/33298/34198/media/eqn-img_14.gif)
Since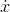 
is continuous, all the values of 
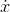occurring inside the sum can differ only infinitesimally from 
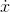(b). Therefore the quantity inside the limit differs only infinitesimally
from 
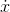(b), and the standard part of its limit must be
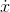(b). 1
2. Suppose f and g are two continuous functions whose derivatives are equal. Then d= f−g is a continuous function whose derivative is zero. But the only continuous function with a derivative of zero is a constant, so f and g differ by at most an additive constant.
3. I’ve established that the derivatives with respect to bof x(b) −x(a) and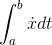 
are the same, so they differ by at most an additive constant.
But at b= a, they’re both zero, so the constant must be zero.
- 1569 reads
