The intermediate value theorem

It seems like a model of mathematical rigor, but there’s a flaw in the reasoning, which is that he assumes without justififcation that the circles do have a point in common. To see that this is not as secure an assumption as it seems, consider the usual Cartesian representation of plane geometry in terms of coordinates (x, y). Usually we assume that x and yare real numbers. What if we instead do our Cartesian geometry using rational numbers as coordinates? Euclid’s five postulates are all consistent with this. For example, circles do exist. Let A = (0, 0) and B = (1, 0). Then there are infinitely many pairs of rational numbers in the set that satisfies the definition of the circle centered at A. Examples include (3/5, 4/5) and (−7/25, 24/25). The circle is also continuous in the sense that if I specify a point on it such as (−7/25, 24/25), and a distance that I’m allowed to make as small as I please, say 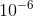, then other points exist on the circle within that distance of the given point. However, the intersection assumed by Euclid’s proof doesn’t exist. It would lie at (1/2, 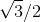), but 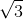doesn’t exist in the rational number system.

In exactly the same way, we can construct counterexamples to the intermediate value theorem if the underlying system of numbers doesn’t have the same properties as the real numbers. For example, let y = 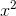. Then y is a continuous function, on the interval from 0 to 1, but if we take the rational numbers as our foundation, then there is no x for√ which y = 1/2. The solution would be x = 1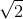, which doesn’t exist in the rational number system. Notice the similarity between this problem and the one in Euclid’s proof. In both cases we have curves that cut one another without having an intersection. In the present example, the curves are the graphs of the functions y = 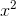and y = 1/2.

The interpretation is that the real numbers are in some sense more densely packed than the rationals, and with two thousand years worth of hindsight, we can see that Euclid should have included a sixth postulate that expressed this density property. One possible way of stating such a postulate is the following. Let L be a ray, and O its endpoint. We think of O as the origin of the positive number line. Let P and Q be sets of points on L such that every point in P is closer to O than every point in Q. Then there exists some point Z on L such that Z lies at least as far from O as every point in P, but no farther than any point in Q. Technically this property is known as completeness. As an example, let P = {x| 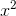<2} and Q = {x| 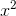   ≥2}. Then the point Z would have to be 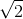, which shows that the rationals are not complete. The reals are complete, and the completeness axiom can serve as one of the fundamental axioms of the real numbers.

Note that the axiom refers to sets P and Q, and says that a certain fact is true for any choice of those sets; it therefore isn’t the type of proposition that is covered by the transfer principle, and in fact it fails for the hyperreals, as we can see if P is the set of all infinitesimals and Q the positive real numbers.

Here is a skeletal proof of the intermediate value theorem, in which I’ll make some simplifying assumptions and leave out some cases. We want to prove that if y is a continuous real-valued function on the real interval from a to b, and if ytakes on values 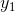and 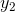at certain points within this interval, then for any 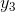between  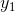and 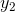 , there is some real x in the interval for which y(x) = 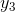. 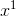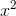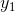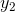I’ll assume the case in which  <  and < .Define sets of real numbers P = {x|y≤ 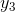}, and let Q = {x|y≥ 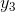 }. For simplicity, I’ll assume that every member of P is less than or equal to every member of Q, which happens, for example, if the function y(x) is always increasing on the interval [a, b]. If P and Q intersect, then the theorem holds. Suppose instead that P and Q do not intersect. Using the completeness axiom, there exists some real x which is greater than or equal to every element of P and less than or equal to every element of Q. Suppose xbelongs to P. Then the following statement is in the right form for the transfer principle to apply to it: for any number x'>x, y(x') >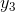 . We can conclude that the statement is also true for the hyperreals, so that if dxis a positive infinitesimal and x'= x+ dx, we have y(x) < 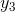, but y(x+ dx) > 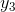. Then by continuity, y(x) −y(x+ dx) is infinitesimal. But y(x) < 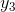 and y(x+ dx) > 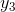, so the standard part of y(x) must equal  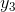. By assumption ytakes on real values for real arguments, so y(x) =  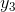. The same reasoning applies if xbelongs to Q, and since xmust belong either to P or to Q, the result is proved.

For an alternative proof of the intermediate value theorem by an entirely different technique, see Keisler (References).

As a side issue, we could ask whether there is anything like the interme- diate value theorem that can be applied to functions on the hyperreals. Our definition of Continuity  explicitly states that it only applies to real functions. Even if we could apply the definition to a function on the hyperreals, the proof given above would fail, since the hyperreals lack the completeness property. As a counterexample, let be some positive infinitesimal, and define a function y such that y = −when st(x) ≤0 and y = everywhere else. If we insist on applying the definition of continuity to this function, it appears to be continuous, so it violates the intermediate value theorem. Note, however, that the way this function is defined is different from the way we usually define functions on the hyperreals. Usually we define a function on the reals, say y = 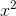, in language to which the transfer principle applies, and then we use the transfer principle to reason about the function’s analog on the hyperreals. For instance, the function y = 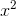 has the property that y≥0 everywhere, and the transfer principle guarantees that that’s also true if we take y = 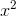 as the definition of a function on the hyperreals.

For functions defined in this way, the intermediate value theorem makes a statement that the transfer principle applies to, and it is therefore true for the hyperreal version of the function as well.