Solutions for chapter 4

Available under Creative Commons-ShareAlike 4.0 International License.

Problem 4.1:

a := 0;

b := 1;

H := 1000;

dt := (b-a)/H;

sum := 0;

t := a;

While (t<=b) [

sum := N(sum+Exp(x^2)*dt);

t := N(t+dt);

]; Echo(sum);

The result is 1.46.

Figure 9.19 h / Problem 2.

Problem 4.2:

The derivative of the cosine is minus the sine, so to get a function whose

derivative is the sine, we need minus the cosine.
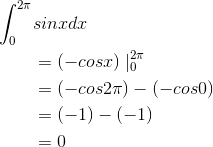
$\begin{align*} \int_{0 }^{2\pi}&sinxdx \\&=(-cosx)\mid _{0 }^{2\pi } \\&=(-cos2\pi )-(-cos0) \\& =(-1)-(-1) \\&=0 \end{align*}$

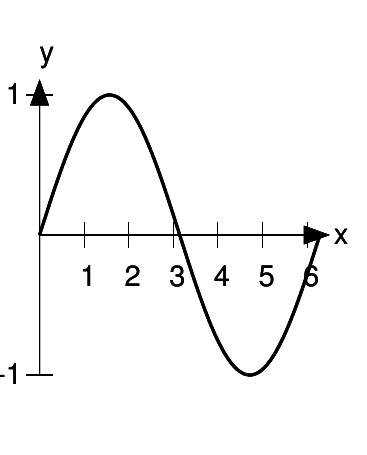
As shown in figure h, the graph has equal amounts of area above and below the xaxis. The area below the axis counts as negative area, so the total is zero.

Problem 4.3:

Figure 9.20 i / Problem 3.

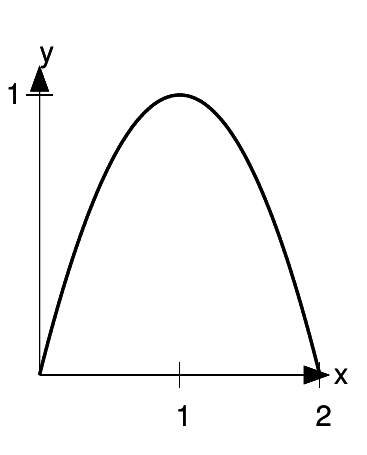
The rectangular area of the graph is 2, and the area under the curve fills a little more than half of that, so let’s guess 1.4.

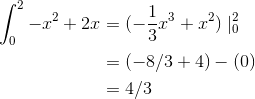
$\begin{align*} \int_{0}^{2}-x^{2}+2x&=(-\frac{1}{3}x^{3}+x^{2})\mid _{0}^{2} \\&=(-8/3+4)-(0) \\ &=4/3 \end{align*}$

This is roughly what we were expecting from our visual estimate.

Problem 4.4:

Over this interval, the value of the sin function varies from 0 to 1, and it spends more time above 1/2 than below it, so we expect the average to be somewhat greater than 1/2. The exact result is

$\begin{align*} \bar{sin}&=\frac{1}{\pi -0}\int_{0}^{\pi }sinxdx \\ &=\frac{1}{\pi}(-cosx)\mid _{0}^{\pi } \\ &=\frac{1}{\pi}[-cos\pi -(-cos0)] \\ &=\frac{2}{\pi} \end{align*}$

which is, as expected, somewhat more than 1/2.

Problem 4.5:

Consider a function y(x) defined on the interval from x= 0 to 2 like this:

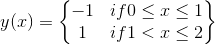
$y(x)=\begin{Bmatrix} -1 &if0\leq x\leq 1 \\ 1& if1< x\leq 2 \end{Bmatrix}$

The mean value of yis zero, but y never equals zero.

Problem 4.6:

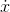Let $\dot{x}$ be defined as

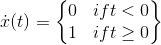
$\dot{x}(t)=\begin{Bmatrix} 0 &ift< 0 \\ 1& ift\geq 0 \end{Bmatrix}$

Integrating this function up to t gives

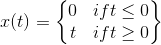
$x(t)=\begin{Bmatrix} 0 & if t\leq 0\\ t& ift\geq 0 \end{Bmatrix}$

The derivative of x at t= 0 is undefined, and therefore integration followed by differentiation doesn’t recover the original function 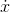$\dot{x}$ .

Problem 4.8:

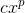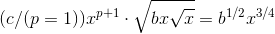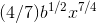First we put the integrand into the more familiar and convenient form $cx^{p}$ , whose integral is $(c/(p=1))x^{p+1}\cdot \sqrt{bx\sqrt{x}}=b^{1/2}x^{3/4}$ Applying the general rule, the result is $(4/7)b^{1/2}x^{7/4}$ .

Problem 4.11:

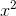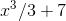The claim is false for indefinite integrals, since indefinite integrals can have a constant of integration. So, for example, a possible indefinite integral of $x^{2}$ is $x^{3}/3+7$ , which is neither even nor odd. The fundamental theorem doesn’t even refer to indefinite integrals, which are simply defined through inverse differentiation.

Let’s fix the claim by changing gto a definite integral, 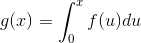$g(x)=\int_{0}^{x}f(u)du$ . The claim is now true. However, the proof still doesn’t quite work. We’ve established that all odd functions have even derivatives, but we haven’t ruled out possibilities such as functions that are neither even nor odd, but that have even derivatives.

2154 reads

You are here

Solutions for chapter 4