(a) The Weierstrass definition requires that if we’re given a particular, and we be able to find a δso small that f(x) + g(x) differs from F+ G by at mostfor |x− a|<δ. But the Weierstrass definition also tells us that given/2, we can find a δsuch that f differs from Fby at most /2, and likewise for gand G. The amount by which f+ gdiffers from F+ Gis then at most/2 +/2, which completes the proof.
(b) Let dxbe infinitesimal. Then the definition of the limit in terms of infinitesimals says that the standard part of f(a + dx) differs at most infinitesimally from F, and likewise for gand G. This means that f+ g differs from F+ Gby the sum of two infinitesimals, which is itself an infinitesimal, and therefore the standard part of f+gevaluated at x+dxequals F+ G, satisfying the definition.
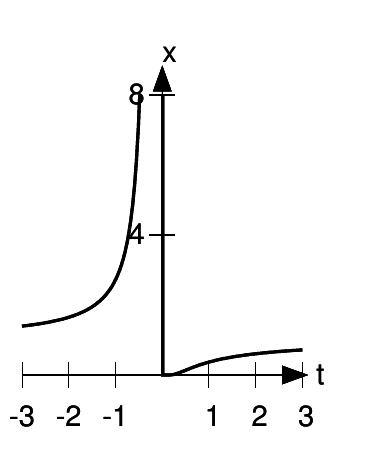
The shape of the graph can be found by considering four cases: large negative x, small negative x, small positive x, and large positive x. In these four cases, the function is respectively close to 1, large, small, and close to 1.
The four limits correspond to the four cases described above.
All five of these can be done using l’Hˆopital’s rule:
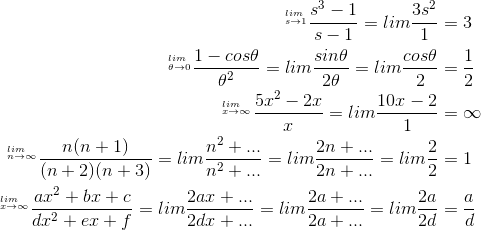
In examples 2, 4, and 5, we differentiate more than once in order to get an expression that can be evaluated by substitution. In 4 and 5, . . . represents terms that we anticipate will go away after the second differentiation. Most people probably would not bother with l’Hˆopital’s rule for 3, 4, or 5, being content merely to observe the behavior of the highest-order term, which makes the limiting behavior obvious. Examples 3, 4, and 5 can also be done rigorously without l’Hˆopit rule, by algebraic manipulation; we divide on the top and bottom by the highest power of the variable, giving an expression that is no longer an indeterminate form ∞/∞.
Both numerator and denominator go to zero, so we can apply l’Hˆopital’s rule. Differentiating top and bottom gives (cos x−xsin x)/(−ln 2
·
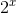), which equals
−1/ln2 at x= 0. To check this numerically, we plug x= 
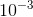into the original expression. The result is −1.44219, which is very close to −1/ln2 =
−1.44269 ....
L’Hˆopital’s rule only works when both the numerator and the denominator go to zero.
Applying l’Hˆopital’s rule once gives
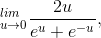
which is still an indeterminate form. Applying the rule a second time, we get
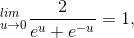
As a numerical check, plugging u= 0.01 into the original expression results in 0.9999917.
L’Hˆopital’s rule gives cos t/1 →−1. Plugging in t= 3.1 gives -0.9997.
Let u= 1/x. Then
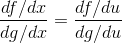
simply by algebraic manipulation of the infinitesimals. (If we want to interpret these quantities as derivatives, then our notational convention is that they stand for the standard parts of the quotients of the infinitesimals, in which case the equality is only for the standard parts.) This equality holds not just in the limit but everywhere that the functions are differentiable. The expression on the left is the thing whose limit we’re trying to prove equals lim f/g. The right-hand side is equal to lim f/gby the previously established form of l’Hˆopital’s rule.
By the definition of continuity in terms of infinitesimals, the function is continuous, because an infinitesimal change dxleads to a change dy= a dxi n the output of the function which is likewise infinitesimals. (This depends on the fact that ais assumed to be real, which implies that it is finite.)
Continuity in terms of the Weierstrass limit holds because we can take
δ= /a.
- 1546 reads
