We can define the sequence f(n) as converging to `if the following is true: for any real number, there exists an integer Nsuch that for all n
greater than N, the value of flies within the range from 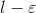 to
to 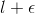 .
.
(a) The convergence of the series is defined in terms of the convergence of its partial sums, which are 1, 0, 1, 0, . . . In the notation used in the definition given in the solution to problem 1 above, suppose we pick= 1/4. Then there is clearly no way to choose any numbers `and N that would satisfy the definition, for regardless of N, `would have to be both greater than 3/4 and less than 1/4 in order to agree with the zeroes and ones that occur beyond the Nth member of the sequence.
(b) As remarked on page 106, the axioms of the real number system, such as associativity, only deal with finite sums, not infinite ones. To see that absurd conclusions result from attempting to apply them to infinite sums, consider that by the same type of argument we could group the sum as 1 + (−1 + 1) + (−1 + 1) + ..., which would equal 1.
The quantity 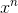 can be reexpressed as
can be reexpressed as 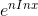 , where ln xis negative by hypothesis. The integral of this
exponential with respect to n is a similar exponential with a constant factor in front, and this converges as
napproaches infinity.
, where ln xis negative by hypothesis. The integral of this
exponential with respect to n is a similar exponential with a constant factor in front, and this converges as
napproaches infinity.
(a) Applying the integral test, we find that the integral of 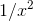 is
-1/x, which converges as xapproaches infinity, so the series converges as well.
is
-1/x, which converges as xapproaches infinity, so the series converges as well.
(b) This is an alternating series whose terms approach zero, so it con-verges. However, the terms get small extremely slowly, so an extraordinarily large number of terms would be required in order to get any kind of decent approximation to the sum. In fact, it is impossible to carry out a straightforward numerical evaluation of this sum because it would require such an enormous number of terms that the rounding errors would overwhelm the result.
(c) This converges by the ratio test, because the ratio of successive terms approaches 0.
(d) Split the sum into two sums, one for the 1103 term and one for the 26390k. The ratio of the two factorials is always less than 44k, so discarding constant factors, the
first sum is less than a geometric series with 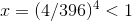 , and
must therefore converge. The second sum is less than a series of the form
, and
must therefore converge. The second sum is less than a series of the form 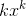 . This one also converges, by the integral test. (It has to be integrated with respect to k, not x, and the
integration can be done by parts.) Since both separate sums converge, the entire sum converges. This bizarre-looking expression was formulated and shown to equal 1/πby the self-taught
genius Srinivasa Ramanujan (1887-1920).
. This one also converges, by the integral test. (It has to be integrated with respect to k, not x, and the
integration can be done by parts.) Since both separate sums converge, the entire sum converges. This bizarre-looking expression was formulated and shown to equal 1/πby the self-taught
genius Srinivasa Ramanujan (1887-1920).
E.g., 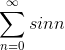 diverges, but the ratio test won’t
establish that, because the limit
diverges, but the ratio test won’t
establish that, because the limit 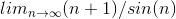 | does not exist.
| does not exist.
The n th term 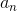 can be rewritten as
2/[n(n+1)], and using partial fractions this can be changed into 2/n−2/(n+ 1). Let the partial sums be
can be rewritten as
2/[n(n+1)], and using partial fractions this can be changed into 2/n−2/(n+ 1). Let the partial sums be 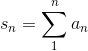 . For insight, let’s write out s3 :
. For insight, let’s write out s3 :
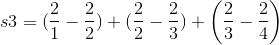
This is called a telescoping series. The second part of one term cancels out with the first part of the next. Therefore we have
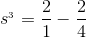
and in general
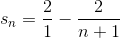
Letting n→∞, we find that the series sums to 2.
Yes, it converges. To see this, consider that its graph consists of a series of peaks and valleys, each of which is narrower than the last and therefore has less area. In fact, the width of these humps approaches zero, so that the area approaches zero. This means that the integral can be represented as a decreasing, alternating series that approaches zero, which must converge.
There are certainly some special values of x for which it does converge, such as 0 and π. For a general value of x, however, things become more complicated. Let the nth term be given by the function t(n). |t|converges to a limit, since the first application of the sine function brings us into the range 0 ≤|t|≤1, and from then on, |t|is decreasing and bounded below by 0. It can’t approach a nonzero limit, for given such a limit t*, there would always be values of t slightly greater than t*such that sin twas less than t*. Therefore the terms in the sum approach zero. This is necessary but not sufficient for the series to converge.
Once t gets small enough, we can approximate the sine using a Taylor series. Approximating the discrete function tby a continuous one, we have 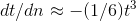 , which can be rewritten as
, which can be rewritten as 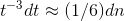 . This is known as separation of variables.
Integrating, we find that at large values of n, where the constant of integration becomes negligible,
. This is known as separation of variables.
Integrating, we find that at large values of n, where the constant of integration becomes negligible, 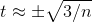 . The sum diverges by the integral test. Therefore the sum diverges for all values of xexcept for multiples of
π, which cause t to hit zero immediately without passing through the region where the Taylor series is a good approximation.
. The sum diverges by the integral test. Therefore the sum diverges for all values of xexcept for multiples of
π, which cause t to hit zero immediately without passing through the region where the Taylor series is a good approximation.
Our first impression is that it must converge, since the 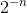 factor shrinks much more rapidly than the
factor shrinks much more rapidly than the 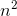 factor. To prove this rigorously, we can apply the integral test. The relevant improper integral was carried out in problem 4 on
p. 104.
factor. To prove this rigorously, we can apply the integral test. The relevant improper integral was carried out in problem 4 on
p. 104.
Finding the sum is far more difficult, and there is no obvious technique that is guaranteed to work. However, the integral test suggests an ap- proach that does lead to a solution. The fact that the indefinite integral can be evaluated suggests that perhaps the partial sum
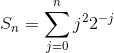
can also be evaluated. Furthermore, the fact that the integral was of the form 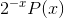 , for some polynomial x, suggests that perhaps
, for some polynomial x, suggests that perhaps 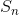 is of the same form. Based on this conjecture, we try to determine the unknown coefficients in
is of the same form. Based on this conjecture, we try to determine the unknown coefficients in 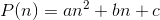
![\begin{align*} S_{n}-S_{n-1}&=n^{2}2^{-n} \\n^{2}2^{-n}&=2^{-n}[-an^{2}+(4a-b)n-2a+2b-c] \end{align*}](/system/files/resource/33/33298/34212/media/eqn-img_42.gif)
Solving for a, b, and c results in P(n) = 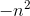 −4n−6. This gives the correct value for the difference
−4n−6. This gives the correct value for the difference 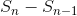 , but doesn’t give
, but doesn’t give 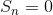 as it should. But this is easy to fix simply by changing the form of our conjectured partial sum slightly to
as it should. But this is easy to fix simply by changing the form of our conjectured partial sum slightly to
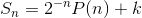 , where k= 6. Evaluating
, where k= 6. Evaluating
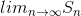 , we get 6.
, we get 6.
The function 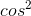 averages to 1/2, so we might naively expect
that cosnwould average to about
averages to 1/2, so we might naively expect
that cosnwould average to about 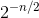 , in which case
the sum would converge for any value of p whatsoever. But the average is misleading, because there are some “lucky” values of nfor which cos2 n≈1, and these
will have a disproportionate effect on the sum. We know by the integral test that
, in which case
the sum would converge for any value of p whatsoever. But the average is misleading, because there are some “lucky” values of nfor which cos2 n≈1, and these
will have a disproportionate effect on the sum. We know by the integral test that 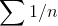 diverges, but
diverges, but 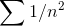 converges, so clearly if p≥2, then even these occasional “lucky” terms will not cause divergence.
converges, so clearly if p≥2, then even these occasional “lucky” terms will not cause divergence.
What about p= 1? Suppose we have some value of n for which 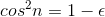 , where is some small number. If this is to happen, then we must have n= kπ+ δ, where
kis an integer and δis small, so that
, where is some small number. If this is to happen, then we must have n= kπ+ δ, where
kis an integer and δis small, so that 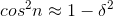 , i.e.,
, i.e.,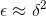 . This occurs with a probability proportional to δ, and the resulting contribution to the sum is
about
. This occurs with a probability proportional to δ, and the resulting contribution to the sum is
about 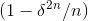 , which by the binomial
theorem is roughly of order of 1/n if
, which by the binomial
theorem is roughly of order of 1/n if 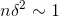 . This
happens with probabilityI
. This
happens with probabilityI 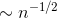 , so the expected value of the
nth term is
, so the expected value of the
nth term is 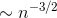 . Since
. Since 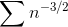 converges by the integral test, this suggests, but does not prove
rigorously, that we also get convergence for
converges by the integral test, this suggests, but does not prove
rigorously, that we also get convergence for
p= 1.
A similar argument suggests that the sum diverges for p= 0.
- 2905 reads






