Problem 8.9
First we rewrite the integrand as
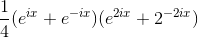
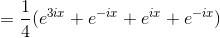
The indefinite integral is
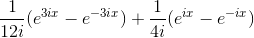
Evaluating this at 0 gives 0, while at =2 we nd 1/3. The result is 1/3.
Problem 8.8
![\begin{align*} sin(a+b)&=(e^{i(a+b)}-e^{-i(a+b)})/2i=(e^{ia}e^{ib}-e^{-ia}e^{-ib})/2i \\&=[(cosa+isina)(cosb+isinb)-(cosa-isina)(cosb-isinb)]/2i \\&=[(cosa+isina)(cosb+isinb)-(cosa-isina)(cosb-isinb)]/2i \\&=cosasinb+isinacosb \end{align*}](/system/files/resource/33/33298/34447/media/eqn-img_25.gif)
By a similar computation, we nd cos(a + b) = cos a cos b - sin a sin b.
Problem 8.10
If 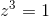 , then we know that |z|= 1, since
cubing zcubes its magnitude. Cubing ztriples its argument, so the argument of zmust be a number that, when tripled, is equivalent to an angle of zero. There are three
possibilities: 0 ×3 = 0, (2π/3) ×3 = 2π, and (4π/3)×3 = 4π. (Other possibilities, such as
(32π/3), are equivalent to one of these.) The solutions are:
, then we know that |z|= 1, since
cubing zcubes its magnitude. Cubing ztriples its argument, so the argument of zmust be a number that, when tripled, is equivalent to an angle of zero. There are three
possibilities: 0 ×3 = 0, (2π/3) ×3 = 2π, and (4π/3)×3 = 4π. (Other possibilities, such as
(32π/3), are equivalent to one of these.) The solutions are:
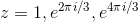
We can think of this as a polynomial in xor a polynomial in y— their roles are symmetric. Let’s call xthe variable. By the fundamental theorem of algebra, it must be
possible to factor it into a product of three linear factors, if the coefficients are allowed to be complex. Each of these factors causes the product to be zero for a certain value of
x. But the condition for the expression to be zero is x3 = y3 , which basically means that the ratio of xto ymust be a third root of 1. The problem,
then, boils down to finding the three third roots of 1, as in problem 10. Using the result of that problem, we find that there are zeroes when x/y equals 1, 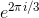 , and
, and 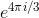 . This tells us that the factorization is
. This tells us that the factorization is 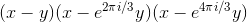 .
.
The second part of the problem asks us to factorize as much as possible using real coefficients. Our only hope of doing this is to multiply out the two factors that involve complex
coefficients, and see if they produce something real. In fact, we can anticipate that it will work, because the coefficients are complex conjugates of one another, and when a quadratic has two
complex roots, they are conjugates. The result is 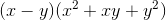 .
.
Applying the differential equation to the form suggested gives 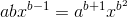 . The exponents must be equal on both sides, so b must be a solution of
. The exponents must be equal on both sides, so b must be a solution of 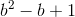 . The solutions are
. The solutions are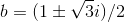 . For a more detailed discussion of this cute problem, see
mathoverflow.net/questions/111066.
. For a more detailed discussion of this cute problem, see
mathoverflow.net/questions/111066.
(a) Let m= 10, 000. We know that integrals of this form can be done, at least in theory, using partial fractions. The ten thousand roots of the polynomial will be ten thousand points
evenly spaced around the unit circle in the complex plane. They can be expressed as 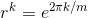 for k= 0 to m−1. Since all the roots are unequal, the partial-fraction form of the integrand contains
only terms of the form
for k= 0 to m−1. Since all the roots are unequal, the partial-fraction form of the integrand contains
only terms of the form 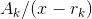 . Integrating, we would get a sum
of ten thousand terms of the form
. Integrating, we would get a sum
of ten thousand terms of the form 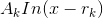 .
.
(b) I tried inputting the integral into three different pieces of symbolic math software: the open-source packages Yacas and Maxima, and the web-based interface to Wolfram’s proprietary Mathematica software at integrals.com. Maxima gave a partially integrated result after a couple of minutes of computation. Yacas crashed. Mathematica’s web interface timed out and suggested buying a stand-alone copy of Mathematica. All three programs probably embarked on the computation of the Ak by attempting to solve 10,000 equations in the 10,000 unknowns Ak, and then ran out of resources (either memory or CPU time).
(c) The expressions look nicer if we let 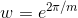 , so
that
, so
that 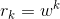 . The residue method gives
. The residue method gives
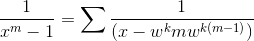
Integration gives
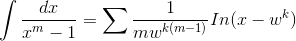
(Thanks to math.stackexchage.com user zulon for suggesting the residue mathod, and to Robert Israel for pointing out that for|x|<1 this can also be expressed as a hypergeometric function:
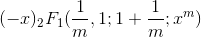
- 2862 reads






