Suppose that the mean value theorem is violated. Let Lbe the set of all xin the interval from ato bsuch that y(x) <
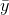 , and likewise let Mbe the set with
y(x) >
, and likewise let Mbe the set with
y(x) > 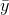 . If the theorem is
violated, then the union of these two sets covers the entire interval from ato b. Neither one can be empty; if, for example, M was empty, then we would have
y<
. If the theorem is
violated, then the union of these two sets covers the entire interval from ato b. Neither one can be empty; if, for example, M was empty, then we would have
y<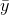 everywhere and also
everywhere and also 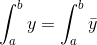 , but it follows directly from the definition of
the definite integral that when one function is less than another, its integral is also less than the other’s. Since y takes on values less than and greater than
, but it follows directly from the definition of
the definite integral that when one function is less than another, its integral is also less than the other’s. Since y takes on values less than and greater than 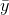 , it follows from the intermediate value theorem that y takes on the
value
, it follows from the intermediate value theorem that y takes on the
value 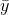 somewhere (intuitively, at a boundary between
L and M).
somewhere (intuitively, at a boundary between
L and M).
- 2467 reads






