It follows immediately from the definition of the derivative that multiplying a function by a constant multiplies its derivative by the same constant, so for example since we know that the
derivative of 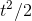 is
is 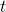 , we can immediately tell that the derivative of
, we can immediately tell that the derivative of 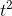 is
is 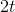 , and the derivative of
, and the derivative of 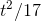 is
is 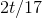 .
.
Also, if we add two functions, their derivatives add. To give a good example of this, we need to have another function that we can differentiate, one that isn't just some multiple of 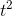 . An easy one is
. An easy one is 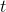 : the derivative of
: the derivative of 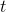 is 1,
since the graph of
is 1,
since the graph of 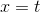 is a line with a slope of 1, and the tangent
line lies right on top of the original line.
is a line with a slope of 1, and the tangent
line lies right on top of the original line.
Example
The derivative of 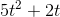 is the derivative of
is the derivative of 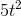 plus the derivative of
plus the derivative of 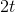 , since derivatives add. The derivative of
, since derivatives add. The derivative of 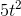 is 5 times the derivative of
is 5 times the derivative of 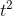 , and the derivative of
, and the derivative of 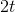 is 2 times the derivative of
is 2 times the derivative of 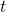 , so putting everything together, we find that the derivative of
, so putting everything together, we find that the derivative of 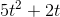 is
is 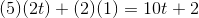 . The derivative of a constant is zero, since a constant function's graph is a horizontal line, with a slope of zero. We now
know enough to differentiate any second order polynomial.
. The derivative of a constant is zero, since a constant function's graph is a horizontal line, with a slope of zero. We now
know enough to differentiate any second order polynomial.
Example
An insect pest from the United States is inadvertently released in a village in rural China. The pests spread outward at a rate of  kilometers per year, forming a widening circle of contagion. Find the number of square kilometers per year that become newly
infested. Check that the units of the result make sense. Interpret the result.
kilometers per year, forming a widening circle of contagion. Find the number of square kilometers per year that become newly
infested. Check that the units of the result make sense. Interpret the result.
Let 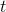 be the time, in years, since the pest was introduced. The
radius of the circle is
be the time, in years, since the pest was introduced. The
radius of the circle is 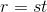 , and its area is
, and its area is 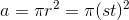 . To make this look like a polynomial, we have to rewrite
it as
. To make this look like a polynomial, we have to rewrite
it as 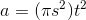 . The derivative is
. The derivative is
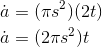
The units of  are km/year, so squaring it gives
are km/year, so squaring it gives 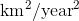 . The 2 and the
. The 2 and the 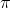 are unitless, and multiplying by
are unitless, and multiplying by 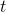 gives units of
gives units of 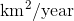 , which is what we expect for
, which is what we expect for 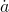 , since it represents the number of square kilometers per year that become infested.
, since it represents the number of square kilometers per year that become infested.
Interpreting the result, we notice a couple of things. First, the rate of infestation isn’t constant; it’s proportional to 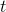 , so people might not pay so
much attention at first, but later on the effort required to combat the problem will grow more and more quickly. Second, we notice that the result is proportional to
, so people might not pay so
much attention at first, but later on the effort required to combat the problem will grow more and more quickly. Second, we notice that the result is proportional to 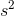 . This suggests that anything that could be done to reduce
. This suggests that anything that could be done to reduce  would be very helpful. For
instance, a measure that cut
would be very helpful. For
instance, a measure that cut  in half would reduce
in half would reduce 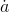 by a factor of four.
by a factor of four.
- 3222 reads






