So far, we have the following results for polynomials up to order
|
function |
derivative |
| 1 | 0 |
| t | 1 |
|
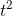
2t |
Interpreting 1 as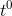 
, we detect what seems to be a general rule, which
is that the derivative of 
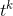is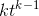 
.
The proof is straightforward but not very illuminating if carried out with the methods developed in this chapter, so I've relegated it to Derivatives of polynomials. It can be proved much more easily using the methods of To infinity — and beyond!.
Example
If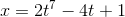 
, find 
.
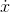This is similar to Example, the only difference being that
we can now handle higher powers of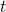 
. The derivative of 
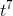is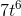 
, so we have
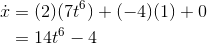
Example
Calculate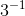 
and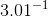 
. Does this seem consistent with a conjecture that the rule for differentiating
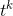holds for k < 0?
We have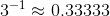 
and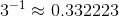 
, the difference being 
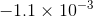. This suggests that the graph of 
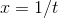has a tangent line at 
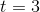with a slope of about
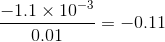
If the rule for differentiating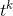 
were to hold, then we would have
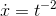, and evaluating this at x = 3 would give -1/9, which
is indeed about -0.11. Yes, the rule does appear to hold for negative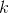 
, although this numerical check does not constitute a proof. A proof is given in Example.
- 1865 reads
