I described how Galileo and Newton found that an object subject to an external force, starting from rest, would have a velocity 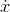 that was proportional to
that was proportional to 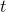 , and a position
, and a position 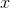 that varied like
that varied like 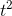 . The proportionality constant for the velocity is called the acceleration,
. The proportionality constant for the velocity is called the acceleration,  , so that
, so that 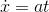 and
and 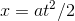 . For example, a sports car accelerating from a stop sign would have a large acceleration, and its velocity
. For example, a sports car accelerating from a stop sign would have a large acceleration, and its velocity 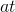 at a given time would therefore be a large number. The acceleration can be thought
of as the derivative of the derivative of
at a given time would therefore be a large number. The acceleration can be thought
of as the derivative of the derivative of 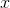 , written
, written 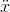 , with two dots. In our example,
, with two dots. In our example, 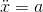 . In general, the acceleration doesn't need to be constant. For example, the sports car
will eventually have to stop accelerating, perhaps because the backward force of air friction becomes as great as the force pushing it forward. The
total force acting on the car would then be zero, and the car would continue in motion at a constant speed.
. In general, the acceleration doesn't need to be constant. For example, the sports car
will eventually have to stop accelerating, perhaps because the backward force of air friction becomes as great as the force pushing it forward. The
total force acting on the car would then be zero, and the car would continue in motion at a constant speed.
Example
Suppose the pilot of a blimp has just turned on the motor that runs its propeller, and the propeller is spinning up. The resulting force on the blimp is therefore increasing steadily, and
let’s say that this causes the blimp to have an acceleration 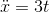 , which increases steadily with time. We want to find the blimp’s velocity and position as functions of time.
, which increases steadily with time. We want to find the blimp’s velocity and position as functions of time.
For the velocity, we need a polynomial whose derivative is 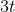 . We
know that the derivative of
. We
know that the derivative of 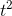 is
is 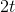 , so we need to use a function that’s bigger by a factor of
, so we need to use a function that’s bigger by a factor of 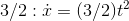 . In fact, we could add any constant to this, and make it
. In fact, we could add any constant to this, and make it
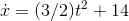 , for example, where the 14 would represent the
blimp’s initial velocity. But since the blimp has been sitting dead in the air until the motor started working, we can assume the initial velocity was zero. Remember, any time you’re working
backwards like this to find a function whose derivative is some other function (integrating, in other words), there is the possibility of adding on a constant like this.
, for example, where the 14 would represent the
blimp’s initial velocity. But since the blimp has been sitting dead in the air until the motor started working, we can assume the initial velocity was zero. Remember, any time you’re working
backwards like this to find a function whose derivative is some other function (integrating, in other words), there is the possibility of adding on a constant like this.
Finally, for the position, we need something whose derivative is 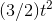 . The derivative of
. The derivative of 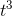 would be
would be 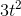 , so we need something half as big as this:
, so we need something half as big as this: 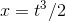 .
.
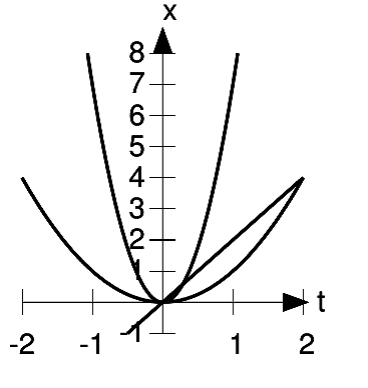
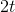 ,
, 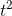 and
and 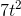 .
.
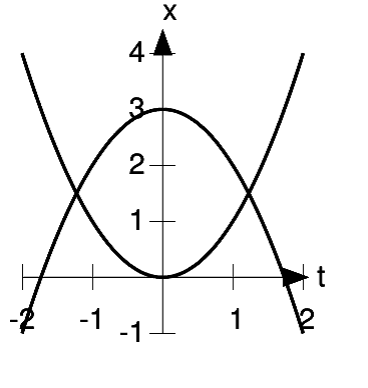
The second derivative can be interpreted as a measure of the curvature of the graph, as shown in Figure 1.11. The graph of the function 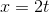 is a line, with no curvature. Its first derivative is 2, and its second derivative is zero. The function
is a line, with no curvature. Its first derivative is 2, and its second derivative is zero. The function 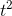 has a second derivative of 2, and the more tightly curved function
has a second derivative of 2, and the more tightly curved function 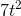 has a bigger second derivative,14.
has a bigger second derivative,14.
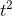 and
and 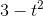
Positive and negative signs of the second derivative indicate concavity. In Figure 1.12, the function 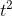 is like a cup with its
mouth pointing up. We say that it's "concave up," and this corresponds to its positive second derivative. The function
is like a cup with its
mouth pointing up. We say that it's "concave up," and this corresponds to its positive second derivative. The function 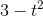 , with a second derivative less than zero, is concave down. Another way of saying it is that if you're driving along a road shaped
like
, with a second derivative less than zero, is concave down. Another way of saying it is that if you're driving along a road shaped
like 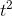 , going in the direction of increasing
, going in the direction of increasing 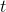 , then your steering wheel is turned to the left, whereas on a road shaped like
, then your steering wheel is turned to the left, whereas on a road shaped like 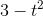 it's turned to the right.
it's turned to the right.
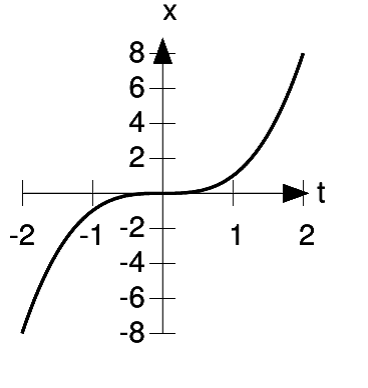
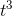 has an inflection point at
has an inflection point at 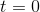
Figure 1.13 shows a
third possibility. The function 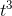 has a derivative
has a derivative 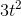 , which equals zero at
, which equals zero at 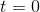 . This called a point of inflection. The concavity of the graph is down on the left, up on the right. The inflection point is
where it switches from one concavity to the other. In the alternative description in terms of the steering wheel, the inflection point is where your steering wheel is crossing from left to
right.
. This called a point of inflection. The concavity of the graph is down on the left, up on the right. The inflection point is
where it switches from one concavity to the other. In the alternative description in terms of the steering wheel, the inflection point is where your steering wheel is crossing from left to
right.
- 3106 reads






