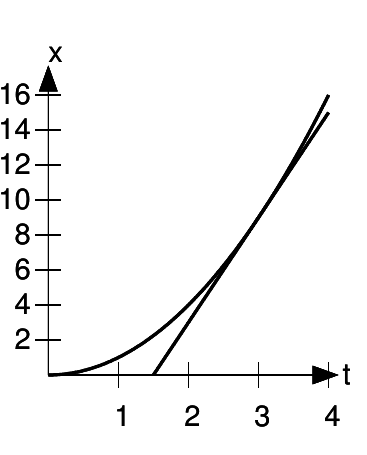
The tangent line has to pass through the point (3,9), and it also seems, at least approximately, to pass through (1.5,0). This gives it a slope of (9 −0)/(3 −1.5) = 9/1.5 = 6, and that’s exactly what 2t is at t= 3.
The tangent line has to pass through the point (0, sin(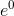 )) = (0, 0.84), and it also seems, at least approximately, to pass through (-1.6,0). This gives it a slope of (0.84 −0)/(0 −(−1.6)) = 0.84/1.6 =
0.53. The more accurate result given in the problem can be found using the methods of To infinity —
and beyond!.
)) = (0, 0.84), and it also seems, at least approximately, to pass through (-1.6,0). This gives it a slope of (0.84 −0)/(0 −(−1.6)) = 0.84/1.6 =
0.53. The more accurate result given in the problem can be found using the methods of To infinity —
and beyond!.
The derivative is a rate of change, so the derivatives of the constants
1 and 7, which don’t change, are clearly zero. The derivative can be interpreted geometrically as the slope of the tangent line, and since the functions tand
7tarelines, their derivatives are simply their slopes, 1, and 7. All of these could also have been found using the formula that says the derivative of
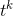 is
is 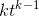 , but it wasn’t really necessary to get that fancy. To find the derivative of
, but it wasn’t really necessary to get that fancy. To find the derivative of
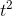 , we can use the formula, which gives 2t. One of the
properties of the derivative is that multiplying a function by a constant multiplies its derivative by the same constant, so the derivative of 7
, we can use the formula, which gives 2t. One of the
properties of the derivative is that multiplying a function by a constant multiplies its derivative by the same constant, so the derivative of 7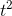 must be (7)(2t) = 14t. By similar reasoning, the derivatives of
must be (7)(2t) = 14t. By similar reasoning, the derivatives of
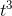 and 7
and 7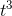 are 3
are 3 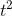 and 21
and 21 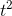 , respectively.
, respectively.
One of the properties of the derivative is that the derivative of a sum is the sum of the derivatives, so we can get this by adding up the derivatives of 3 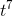 , −4
, −4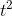 , and 6. The derivatives of the three terms are 21
, and 6. The derivatives of the three terms are 21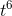 , −8t, and 0, so the derivative of the whole thing is 21
, −8t, and 0, so the derivative of the whole thing is 21 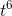 −8t.
−8t.
This is exactly like problem 4, except that instead of explicit numerical constants like 3 and −4, this problem involves symbolic constants a, b, and c. The result is 2at+ b.
The first thing that comes to mind is 3t. Its graph would be a line with a slope of 3, passing through the origin. Any other line with a slope of3 would work too, e.g., 3t+ 1.
Differentiation lowers the power of a monomial by one, so to get something with an exponent of 7, we need to differentiate something with an exponent of 8. The derivative of 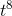 would be 8
would be 8 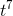 , which is eight times too big, so we really need (
, which is eight times too big, so we really need (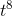 /8). As in problem 6, any other function that differed by an additive
constant would also work, e.g., (
/8). As in problem 6, any other function that differed by an additive
constant would also work, e.g., ( 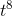 / 8) + 1.
/ 8) + 1.
This is just like problem 7, but we need something whose derivative is three times bigger. Since multiplying by a constant multiplies the derivative by the same constant, the way to accomplish
this is to take the answer to problem 7, and multiply by three. A possible answer is (3/8) 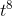 , or that function plus any constant.
, or that function plus any constant.
This is just a slight generalization of problem 8. Since the derivative of a sum is the sum of the derivatives, we just need to handle each term individually, and then add up the results. The
answer is (3/8) 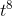 −(4/3)
−(4/3) 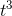 + 6t, or that function plus any constant.
+ 6t, or that function plus any constant.
The function v = (4/3)π 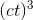 looks scary
and complicated, but it’s nothing more than a constant multiplied by
looks scary
and complicated, but it’s nothing more than a constant multiplied by 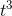 , if we rewrite it as v= (4/3)π
, if we rewrite it as v= (4/3)π 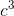
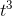 . The whole thing in square brackets is simply one big constant, which just comes along for the ride when we differentiate. The
result is v˙ = (4/3)π
. The whole thing in square brackets is simply one big constant, which just comes along for the ride when we differentiate. The
result is v˙ = (4/3)π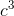 (3
(3 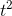 ), or, simplifying, v˙ = 4π
), or, simplifying, v˙ = 4π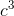
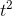 . (For further physical insight, we can factor this as 4π
. (For further physical insight, we can factor this as 4π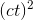 c, where ct is the radius of the expanding sphere, and the part in brackets is the sphere’s surface area.)
c, where ct is the radius of the expanding sphere, and the part in brackets is the sphere’s surface area.)
For purposes of checking the units, we can ignore the unit- less constant 4π, which just leaves 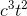 . This has units of
. This has units of 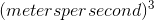
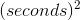 , which works out to be cubic meters per second. That makes sense, because it tells us how quickly a volume is increasing over
time.
, which works out to be cubic meters per second. That makes sense, because it tells us how quickly a volume is increasing over
time.
This is similar to problem 10, in that it looks scary, but we can rewrite it as a simple monomial,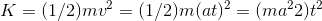 . The derivative is
. The derivative is 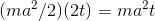 . The car needs more and more power to accelerate as its speed increases.
. The car needs more and more power to accelerate as its speed increases.
To check the units, we just need to show that the expression 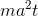 has units that are like those of the original expression for K, but divided by seconds, since it’s a rate of change
of K over time. This indeed works out, since the only change in the factors that aren’t unitless is the reduction of the powet of t from 2 to 1.
has units that are like those of the original expression for K, but divided by seconds, since it’s a rate of change
of K over time. This indeed works out, since the only change in the factors that aren’t unitless is the reduction of the powet of t from 2 to 1.
The area is 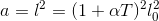 To make this into
something we know how to differentiate, we need to square out the expression involving T, and make it into something that is expressed explicitly as a polynomial:
To make this into
something we know how to differentiate, we need to square out the expression involving T, and make it into something that is expressed explicitly as a polynomial:
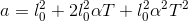
Now this is just like problem 5, except that the constants superficially look more complicated. The result is
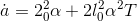
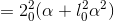
We expect the units of the result to be area per unit temperature, e.g., degrees per square meter. This is a little tricky, because we have to figure out what units are implied for the constant
α. Since the question talks about 1 + αT, apparently the quantity αTis unitless. (The 1 is unitless, and you can’t add things that have different
units.) Therefore the units of α must be “per degree,” or inverse degrees. It wouldn’t make sense to add α and 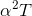 unless they had the same units (and you can check for yourself that they do), so the
whole thing inside the parentheses must have units of inverse degrees. Multiplying by the
unless they had the same units (and you can check for yourself that they do), so the
whole thing inside the parentheses must have units of inverse degrees. Multiplying by the 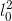 in front, we have units of area per degree, which is what we expected.
in front, we have units of area per degree, which is what we expected.
The first derivative is 6 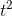 −1. Going again, the answer is
12t.
−1. Going again, the answer is
12t.
The first derivative is 3  +2t, and the second is
6t+2. Setting this equal to zero and solving for t, we find t= −1/3. Looking at the graph, it does look like the concavity is down for
t<−1/3, and up for t>−1/3.
+2t, and the second is
6t+2. Setting this equal to zero and solving for t, we find t= −1/3. Looking at the graph, it does look like the concavity is down for
t<−1/3, and up for t>−1/3.
I chose k = −1, and t = 1. In other words, I’m going to check the slope of the function x = 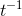 = 1/r at t = 1, and see whether it really equals
= 1/r at t = 1, and see whether it really equals
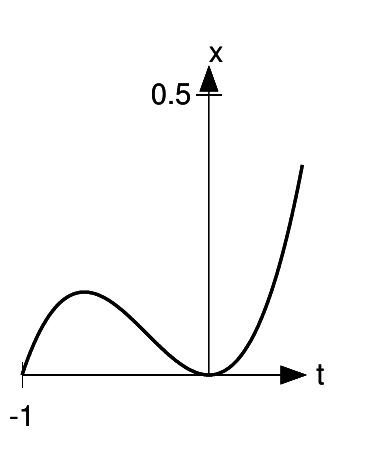
 = −1. Before even doing the graph, I note that the
sign makes sense: the function 1/tis decreasing for t>0, so its slope should indeed be negative.
= −1. Before even doing the graph, I note that the
sign makes sense: the function 1/tis decreasing for t>0, so its slope should indeed be negative.
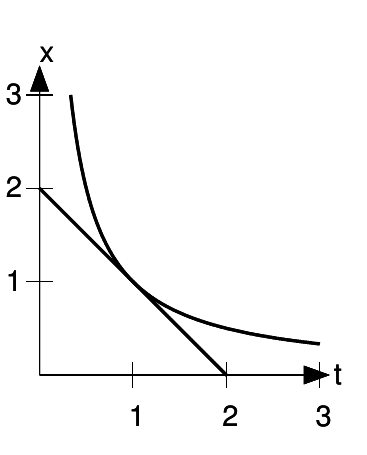
The tangent line seems to connect the points (0,2) and (2,0), so its slope does indeed look like it’s −1.
The problem asked us to consider the logical meaning of the two possible outcomes. If the slope had been significantly different from−1 given the accuracy of our result, the conclusion would have been that it was incorrect to extend the rule to negative values of k. Although our example did come out consistent with the rule, that doesn’t prove the rule in general. An example can disprove a conjecture, but can’t prove it. Of course, if we tried lots and lots of examples, and they all worked, our confidence in the conjecture would be increased.
A minimum would occur where the derivative was zero. First we rewrite the function in a form that we know how to differentiate:
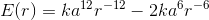
We’re told to have faith that the derivative of 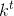 is
is
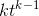 even for k<0, so
even for k<0, so
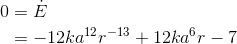
To simplify, we divide both sides by 12k. The left side was already zero, so it keeps being zero.
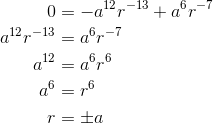
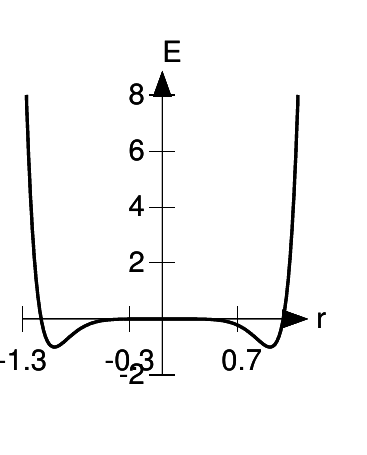
To check that this is a minimum, not a maximum or a point of inflection, one method is to construct a graph. The constants aand kare irrelevant to this issue. Changing ajust rescales the horizontal raxis, and changing kdoes the same for the vertical Eaxis. That means we can arbitrarily set a= 1 and k= 1, and construct the graph shown in the figure. The points r= ±aare now simply r= ±1. From the graph, we can see that they’re clearly minima. Physically, the minimum at r= −acan be interpreted as the same physical configuration of the molecule, but with the positions of the atoms reversed. It makes sense that r= −abehaves the same as r= a, since physically the behavior of the system has to be symmetric, regardless of whether we view it from in front or from behind.
The other method of checking that r= ais a minimum is to take the second derivative. As before, the values of aand kare irrelevant, and can be set to 1. We then have
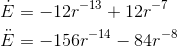
Plugging in r= ±1, we get a positive result, which confirms that the concavity is upward.
Since polynomials don’t have kinks or endpoints in their graphs, the maxima and minima must be points where the derivative is zero. Differentiation bumps down all the powers of a polynomial by one, so the derivative of a third-order polynomial is a second-order polynomial. A second-order polynomial can have at most two real roots (values of tfor which it equals zero), which are given by the quadratic formula. (If the number inside the square root in the quadratic formula is zero or negative, there could be less than two real roots.) That means a third-order polynomial can have at most two maxima or minima.
Since f, g, and sare smooth and defined everywhere, any extrema they possess occur at places where their derivatives are zero. The converse is not necessarily true, however; a place where the derivative is zero could be a point of inflection. The derivative is additive, so if both f and g have zero derivatives at a certain point, sdoes as well. Therefore in most cases, if fand gboth have an extremum at a point, so will s. However, it could happen that this is only a point of inflection for s, so in general, we can’t conclude anything about the extrema of ssimply from knowing where the extrema of f and go ccur.
Going the other direction, we certainly can’t infer anything about extrema of f and g from knowledge of s alone. For example, if s(x) = 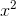 , with a minimum at x= 0, that tells us very little about
fand g. We could have, for example,
, with a minimum at x= 0, that tells us very little about
fand g. We could have, for example, 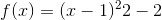 and
and 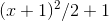 neither of which has an extremum at x = 0.
neither of which has an extremum at x = 0.
Considering Vas a function of h, with btreated as a constant, we have for the slope of its graph
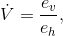
so
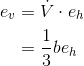
Thinking of the rocket’s height as a function of time, we can see that goal is to measure the function at its maximum. The derivative is zero at the maximum, so the error incurred due to timing is approximately zero. She should not worry about the timing error too much. Other factors are likely to be more important, e.g., the rocket may not rise exactly vertically above the launch pad.
If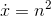 , and xis a polynomial in n, then
, and xis a polynomial in n, then
we must have 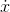 (n) =
x(n) −x(n−1) =
(n) =
x(n) −x(n−1) = 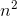 . If xis a polynomial of order k, then x(n) and x(n−1) both have
. If xis a polynomial of order k, then x(n) and x(n−1) both have 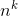 terms with coefficients of 1, so
terms with coefficients of 1, so 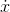 has no
has no 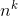 term. We want x˙ to have a nonvanishing
term. We want x˙ to have a nonvanishing 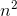 term, so we must have k≥3. For k>3, it’s easy to show that
the
term, so we must have k≥3. For k>3, it’s easy to show that
the 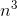 term in x(n)
−x(n−1) is nonzero, so we must have k= 3. Let x(n) = a
term in x(n)
−x(n−1) is nonzero, so we must have k= 3. Let x(n) = a 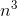 + b
+ b 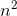 + ..., where ais the coefficient that we want to prove is
1/3, and ...represents lower-order terms. By the binomial theorem, we have x(n−1) = an3
−3a
+ ..., where ais the coefficient that we want to prove is
1/3, and ...represents lower-order terms. By the binomial theorem, we have x(n−1) = an3
−3a 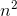 +
b
+
b 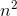 +
..., and subtracting this from x(n) gives
+
..., and subtracting this from x(n) gives 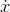 (n) = 3a
(n) = 3a 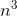 + .... Since 3a= 1, we have a= 1/3.
+ .... Since 3a= 1, we have a= 1/3.
- 2888 reads






