where . . . indicates infinitesimal terms. The derivative is the standard part of this, which is .
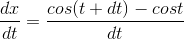
The identity cos(α+ β) = cos αcos β−sin αsin βthen gives
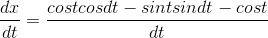
The small-angle approximations cos dt≈1 and sin dt≈dtresult in
| H |
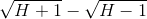
|
| 1000 | .032 |
| 1000,000 | 0.0010 |
| 1000,000,000 | 0.00032 |
The result is getting smaller and smaller, so it seems reasonable to guess that if His infinite, the expression gives an infinitesimal result.
| dx |
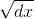
|
| .1 | .23 |
| .001 | .032 |
| .00001 | 0..32 |
The square root is getting smaller, but is not getting smaller as fast as the number itself. In proportion to the original number, the square root is actually getting bigger. It looks
like 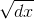 is infinitesimal, but it’s still infinitely big
compared to dx. This makes sense, because
is infinitesimal, but it’s still infinitely big
compared to dx. This makes sense, because 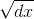 equals
equals
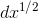 . we already knew that
. we already knew that 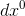 , which equals 1, was infinitely big compared to
, which equals 1, was infinitely big compared to  , which equals dx. In the hierarchy of infinitesimals,
, which equals dx. In the hierarchy of infinitesimals, 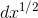 fits in between
fits in between 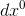 and
and 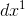 .
.
Statements (a)-(d), and (f )-(g) are all valid for the hyperreals, because they meet the test of being directly translatable, without having to interpret the meaning of things like particular subsets of the reals in the context of the hyperreals.
Statement (e), however, refers to the rational numbers, a particular subset of the reals, and that means that it can’t be mindlessly translated into a statement about the hyperreals, unless we had figured out a way to translate the set of rational numbers into some corresponding subset of the hyperreal numbers like the hyperrationals! This is not the type of statement that the transfer principle deals with. The statement is not true if we try to change “real” to “hyperreal” while leaving “rational” alone; for example, it’s not true that there’s a rational number that lies between the hyperreal numbers 0 and 0 + dx, where dxis infinitesimal.
If 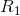 is finite and
is finite and 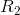 infinite, then 1/
infinite, then 1/ 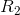 is infinitesimal, 1/
is infinitesimal, 1/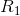 + 1/
+ 1/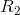 differs infinitesimally from 1/
differs infinitesimally from 1/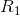 , and the combined resistance R differs infinitesimally from
, and the combined resistance R differs infinitesimally from 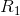 . Physically, the second pipe is blocked or too thin to carry any significant flow, so it’s as though it weren’t present.
. Physically, the second pipe is blocked or too thin to carry any significant flow, so it’s as though it weren’t present.
If 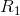 is finite and
is finite and 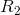 is infinitesimal, then 1/
is infinitesimal, then 1/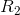 is infinite, 1/
is infinite, 1/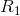 + 1/
+ 1/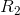 is also infinite, and the combined resistance Ris infinitesimal. It’s so easy for water to flow through
is also infinite, and the combined resistance Ris infinitesimal. It’s so easy for water to flow through 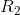 that
that 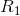 might as well not be present. In the context of electrical circuits rather than water pipes, this is known as a short circuit.
might as well not be present. In the context of electrical circuits rather than water pipes, this is known as a short circuit.
The velocity addition is only interesting if the infinitesimal velocities uand vare comparable to one another, i.e., their ratio is finite. Let’s writefor the size of these
infinitesimals, so that both uand vcan be written asmultiplied by some finite number. Then 1 + uv differs from 1 by an amount that is on the order of 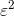 , which is infinitesimally small compared to . The same then
holds true for 1/(1 + uv) as well. The result of velocity addition (u+ v)/(1 + uv) is then u+ v+
..., where ...represents quantities of order
, which is infinitesimally small compared to . The same then
holds true for 1/(1 + uv) as well. The result of velocity addition (u+ v)/(1 + uv) is then u+ v+
..., where ...represents quantities of order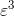 , which are amount to a correction that is infinitesimally small compared to the nonrelativistic
result u+ v.
, which are amount to a correction that is infinitesimally small compared to the nonrelativistic
result u+ v.
This would be a horrible problem if we had to expand this as a polynomial with 101 terms, as in chapter 1! But now we know the chain rule, so it’s easy. The derivative is
![[100(2x+3)^{99}] [2]](/system/files/resource/33/33298/34389/media/eqn-img_33.gif)
where the first factor in brackets is the derivative of the function on the outside, and the second one is the derivative of the “inside stuff.” Simplifying a little, the answer is 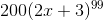 .
.
Applying the product rule, we get
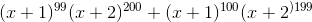
(The chain rule was also required, but in a trivial way — for both of the factors, the derivative of the “inside stuff ” was one.)
The derivative of 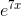 is
is 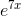 ·7, where the first factor is the derivative of the outside stuff (the
derivative of a base-eexponential is just the same thing), and the second factor is the derivative of the inside stuff. This would normally be written as 7
·7, where the first factor is the derivative of the outside stuff (the
derivative of a base-eexponential is just the same thing), and the second factor is the derivative of the inside stuff. This would normally be written as 7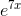 .
.
The derivative of the second function is 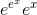 , with
the second exponential factor coming from the chain rule.
, with
the second exponential factor coming from the chain rule.
We need to put together three different ideas here: (1) When a function to be differentiated is multiplied by a constant, the constant just comes along for the ride. (2) The derivative of the sine is the cosine. (3) We need to use the chain rule. The result is −abcos(bx+ c).
If we just wanted to fine the integral of sin x, the answer would be −cos x(or −cos xplus an arbitrary constant), since the derivative would be −(−sin x), which would take us back to the original function. The obvious thing to guess for the integral of asin(bx+ c) would therefore be −acos(bx+ c), which almost works, but not quite. The derivative of this function would be absin(bx+ c), with the pesky factor of bcoming from the chain rule. Therefore what we really wanted was the function −(a/b) cos(bx+ c).
The chain rule gives
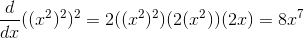
which is the same as the result we would have gotten by differentiating 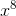 .
.
To find a maximum, we take the derivative and set it equal to zero. The whole factor of 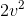 / gin front is just one big constant, so it comes along for the ride. To differentiate the factor of sin θcos
θ, we need to use the chain rule, plus the fact that the derivative of sin is cos, and the derivative of cos is −sin.
/ gin front is just one big constant, so it comes along for the ride. To differentiate the factor of sin θcos
θ, we need to use the chain rule, plus the fact that the derivative of sin is cos, and the derivative of cos is −sin.
We’re interested in angles between, 0 and 90 degrees, for which both the sine and the cosine are positive, so
To check that this is really a maximum, not a minimum or an inflection point, we could resort to the second derivative test, but we know the graph of R(θ) is zero at θ= 0 and θ= 90 ◦, and positive in between, so this must be a maximum.
Taking the derivative and setting it equal to zero, we have 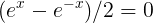 , so
, so 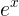 =
= 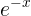 , which occurs only at x = 0. The second derivative is (
, which occurs only at x = 0. The second derivative is ( 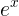 +
+ 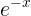 ) /2 (the same as the original function), which is positive for all x, so the function is everywhere concave up,
and this is a minimum.
) /2 (the same as the original function), which is positive for all x, so the function is everywhere concave up,
and this is a minimum.
There are no kinks, endpoints, etc., so extrema will occur only in places where the derivative is zero. Applying the chain rule, we find the derivative to be cos(sin(sin x)) cos(sin x) cos x. This will be zero if any of the three factors is zero. We have cos u= 0 only when |u|≥π/2, and π/2 is greater than 1, so it’s not possible for either of the first two factors to equal zero. The derivative will therefore equal zero if and only if cos x= 0, which happens in the same places where the derivative of sin xis zero, at x= π/2 + πn, where nis an integer.
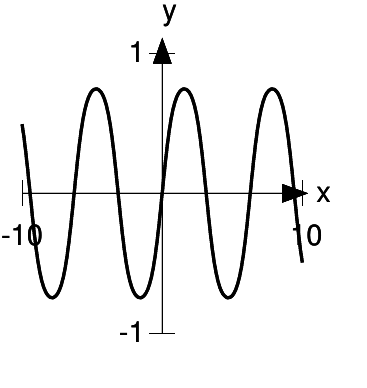
This essentially completes the required demonstration, but there is one more technical issue, which is that it’s conceivable that some of these could be points of inflection. Constructing a graph of sin (sin (sin x)) gives us the necessary insight to see that this can’t be the case. The function essentially looks like the sine function, but its extrema have been “shaved down” a little, giving them slightly flatter tips that don’t quite extend out to ±1. It’s therefore fairly clear that these aren’t points of inflection. To prove this more rigorously, we could take the second derivative and show that it was nonzero at the places where the first derivative is zero. That would be messy. A less tedious argument is as follows. We can tell from its formula that the function is periodic, i.e., it has the property that f(x+ `) = f(x), for `= 2π. This follows because the innermost sine function is periodic, and the outer layers only depend on the result of the inner layer. Therefore all the points of the form π/2 + 2πnhave the same behavior. Either they’re all maxima or they’re all points of inflection. But clearly a function can’t oscillate back and forth without having any maxima at all, so they must all be maxima. A similar argument applies to the minima.
The function fhas a kink at x= 0, so it has no uniquely defined tangent line there, and its derivative at that point is undefined. In terms of infinitesimals, positive values of dxgive df/dx= (dx+ dx)/dx= 2, while negative ones give df/dx = (−dx+ dx)/dx= 0. Since the standard part of the quotient dy/dxdepends on the specific value of dx, the derivative is undefined.
The function ghas no kink at x= 0. The graph of x|x|looks like two half-parabolas glued together, and since both of them have slopes of 0 at x= 0, the slope of the tangent line is well defined, and is zero. In terms of infinitesimals, dg/dyis the standard part of |dx|+ 1, which is 1.
(a) As suggested, let 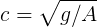 , so that d
= Aln cosh ct= A ln
, so that d
= Aln cosh ct= A ln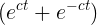 .
Applying the chain rule, the velocity is
.
Applying the chain rule, the velocity is
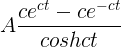
(b) The expression can be rewritten as Actanh ct.
(c) For large t, the 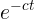 terms become
negligible, so the velocity is
terms become
negligible, so the velocity is 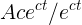 =
Ac. (d) From the original expression, Amust have units of distance, since the logarithm is unitless. Also, since ctoccurs inside a function, ctmust be
unitless, which means that chas units of inverse time. The answers to parts b and c get their units from the factors of Ac, which have units of distance multiplied by inverse
time, or velocity.
=
Ac. (d) From the original expression, Amust have units of distance, since the logarithm is unitless. Also, since ctoccurs inside a function, ctmust be
unitless, which means that chas units of inverse time. The answers to parts b and c get their units from the factors of Ac, which have units of distance multiplied by inverse
time, or velocity.
Since I’ve advocated not memorizing the quotient rule, I’ll do this one from first principles, using the product rule.
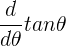
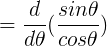
![\large =\frac{d}{d\theta }[sin\theta (cos\theta )^{-1}]](/system/files/resource/33/33298/34389/media/eqn-img_59.gif)
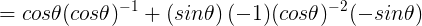
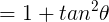
(Using a trig identity, this can also be rewritten as 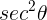 )
)
Reexpressing ![\large \sqrt[3]{x}](/system/files/resource/33/33298/34389/media/eqn-img_63.gif) as
as 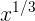 , the derivative is
, the derivative is 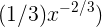 .
.
(a) Using the chain rule, the derivative of 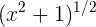 is (1/2)
is (1/2) 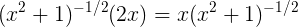
(b) This is the same as a, except that the 1 is replaced with an a2 , so the answer is 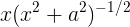 . The idea would be that ahas the same units as x.
. The idea would be that ahas the same units as x.
(c) This can be rewritten as 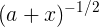 , giving a
derivative of
, giving a
derivative of 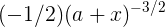
(d) This is similar to c, but we pick up a factor of −2xfrom the chain rule, making the result 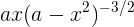 .
.
By the chain rule, the result is 2/(2t+ 1).
Using the product rule, we have
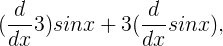
but the derivative of a constant is zero, so the first term goes away, and we get 3 cos x, which is what we would have had just from the usual method of treating multiplicative
constants.
N(Gamma(2))
1
N(Gamma(2.00001))
1.0000042278
N( (1.0000042278-1)/(.00001) )
0.4227799998
Probably only the first few digits of this are reliable.
The area and volume are
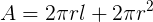
and
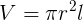 .
.
The strategy is to use the equation for A, which is a constant, to eliminate the variable `, and then maximize Vin terms of r.
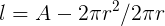
Substituting this expression for `back into the equation for V,
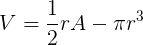
To maximize this with respect to r, we take the derivative and set it equal to zero.
In other words, the length should be the same as the diameter.
(a) We can break the expression down into three factors: the constant m/2 in front, the nonrelativistic velocity dependence 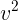 , and the relativistic correction factor
, and the relativistic correction factor 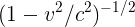 . Rather than substituting in at for v, it’s a little less messy to
calculate dK/dt= (dK/dv)(dv/dt) = adK/dv. Using the product rule, we have
. Rather than substituting in at for v, it’s a little less messy to
calculate dK/dt= (dK/dv)(dv/dt) = adK/dv. Using the product rule, we have
(b) The expression 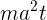 is the nonrelativistic
(classical) result, and has the correct units of kinetic energy divided by time. The factor in square brackets is the relativistic correction, which is unitless.
is the nonrelativistic
(classical) result, and has the correct units of kinetic energy divided by time. The factor in square brackets is the relativistic correction, which is unitless.
(c) As vgets closer and closer to c, the expression 1 −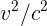 approaches zero, so both the terms in the relativistic correction blow up to positive infinity.
approaches zero, so both the terms in the relativistic correction blow up to positive infinity.
We already know it works for positive x, so we only need to check it for negative x. For negative values of x, the chain rule tells us that the derivative is 1/|x|, multiplied by −1, since d|x|/dx= −1. This gives −1/|x|, which is the same as 1/x, since xis assumed negative.
Since f(x) = f(−x),
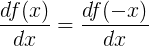
But by the chain rule, the right-hand side equals −f'(x), as claimed.
Let f = 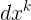 /dx be the
unknown function. Then
/dx be the
unknown function. Then
where we can use the ordinary rule for derivatives of powers on 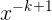 , since −k+ 1 is positive. Solving for f, we have the desired result.
, since −k+ 1 is positive. Solving for f, we have the desired result.
Since the parallel postulate can be expressed in terms of algebra through Cartesian geometry, the transfer principle tells us that it holds for F as well. But G is defined in terms of the finite hyperreals, so statements about E don’t carry over to statements about G simply by replacing “real” with “hyperreal,” and the transfer principle does not guarantee that the parallel postulate applies to G.
In fact, it is easy to find a counterexample in G. Letbe an infinitesimal number. Consider the lines with equations y= 1 and y= 1+x. Neither of these intersects the x axis.
No, it is not valid to associate only E with the plane described by Eu-clid’s axioms. All of Euclid’s axioms hold equally well in F. F is referred to as a nonstandard model of Euclid’s axioms.
It has the same relation to standard Euclidean geometry as the hyperreals have to the reals. If we want to make up a set of axioms that describes E and can’t describe F, then we need to add an
additional axiom to Euclid’s set. An example of such an axiom would be an axiom stating that given any two line segments with lengths 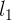 and
and 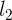 , there exists some integer nsuch that n
, there exists some integer nsuch that n 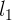 >
> 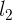 . Note that although this axiom holds in E, the transfer principle cannot be used to show that it holds in F — it is false
in F. The transfer principle doesn’t apply because the transfer principle doesn’t apply to statements that include phrases such as “for any integer.”
. Note that although this axiom holds in E, the transfer principle cannot be used to show that it holds in F — it is false
in F. The transfer principle doesn’t apply because the transfer principle doesn’t apply to statements that include phrases such as “for any integer.”
The normal definition of a repeating decimal such as 0.999 ...is that it is the limit of the sequence 0.9, 0.99, ..., and the limit is a real number, by definition. 0.999 ...equals 1. However, there is an intuition that the limiting process 0.9, 0.99, ...“never quite gets there.” This intuition can, in fact, be formalized in the construction described beginning on page 144; we can define a hyperreal number based on the sequence 0.9, 0.99, ..., and it is a number infinitesimally less than one. This is not, however, the normal way of defining the symbol 0.999 ..., and we probably wouldn’t want to change the definition so that it was. If it was, then 0.333 ...would not equal 1/3.
Converting these into Leibniz notation, we find
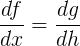
and
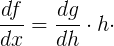
To prove something is not true in general, it suffices to find one counterexample. Suppose that gand hare both unitless, and xhas units of seconds. The value of
fis defined by the output of g, so fmust also be unitless. Since f is unitless, df / dx has units of inverse seconds (“per
second”). But this doesn’t match the units of either of the proposed expressions, because they’re both unitless. The correct chain rule, however, works. In the equation
the right-hand side consists of a unitless factor multiplied by a factor with units of inverse seconds, so its units are inverse seconds, matching the left-hand side.
We can make life a lot easier by observing that the function s(f) will be maximized when the expression inside the square root is minimized. Also, since fis squared
every time it occurs, we can change to a variable x= , and then once the optimal value of xis found we can take its square root in order to find the optimal f.
The function to be optimized is then
Differentiating this and setting the derivative equal to zero, we find
which results in , or
(choosing the positive root, since frepresents a frequencies, and frequencies are positive by definition). Note that the quantity inside the square root involves the square of a frequency, but then we take its square root, so the units of the result turn out to be frequency, which makes sense. We can see that if bis small, the second term is small, and the maximum occurs very nearly at fo .
There is one subtle issue that was glossed over above, which is that the graph on page 51 shows two extrema: a minimum at f= 0 and a maximum at f>0. What happened to the f= 0 minimum? The issue is that I was a little sloppy with the change of variables. Let Istand for the quantity inside the square root in the original expression for s. Then by the chain rule,
We looked for the place where dI/dxwas zero, but ds/dfcould also be zero if one of the other factors was zero. This is what happens at f= 0, where dx/df= 0.
Applying the geometric series 1/(1 + r) = 1 + r+ + ...,
As checks on our result, we note that the units work out correctly (meters squared divided by meters give meters), and that the result is indeed large, since we divide by the small quantity dx.
One way to evaluate an expression like is by
using the identity
=
. If we try to substitute a= 1 and b= ∞, we
get
, which has an indeterminate
form inside the exponential.
One way to express the idea is that if there is even the tiniest error in the value of a, the value of a∞ can have any positive value.
- 3034 reads






