Divergence Revisited

Available under Creative Commons-NonCommercial-ShareAlike 4.0 International License.

Now that we have incorporated human capital and technology into our framework, we can identify some further possible explanations of divergence. Our theory says that economies will converge if they differ only in terms of their initial capital stock. But it is possible that different economies will also have different balanced-growth paths. ***Figure 6.16 "Balanced Growth in Two Countries with Different Ratios of Capital to Output" shows what this looks like. The ratio of capital stock to output in the very long run depends on a number of different factors, including the growth rate of technology and the growth rate of the workforce. If these differ across countries, then their balanced-growth paths will differ as well, and we will not observe convergence. [***The toolkit presents a complete model of balanced growth, including a formula for the balanced-growth ratio of capital stock to output.***]

　

Figure 6.18 Figure 6.16 Balanced Growth in Two Countries with Different Ratios of Capital to Output  

Economies may have different balanced-growth paths. In this example, the ratio of capital stock to output is higher in country A than in country B. 

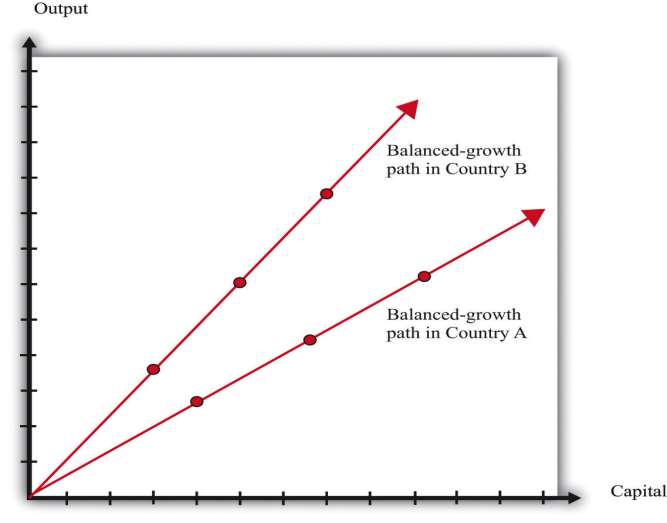
This explanation—and our previous stories of divergence—tells us why different economies will not necessarily end up at exactly the same level of output per worker. But the problem of divergence is in some ways worse than that. Some countries are not only failing to converge but also moving further and further apart. In other words, in some cases, richer economies are growing faster than poorer economies. Indeed, as we saw with Niger, some of the poorest economies in the world have been shrinking rather than growing.

Remember that the growth rate of output per worker on a balanced-growth path is as follows:

We can explain divergence in our framework if human capital or technology is growing more slowly in poor countries than in rich ones. Are there reasons to expect this to be the case? Earlier, we said that countries with low levels of human capital might also be countries where the return to human capital investment was large, which is a force for convergence. We also pointed out, however, that the marginal product of physical capital might be larger in an economy with a superior technology, even if that economy had more capital. The same is true of human capital. Countries can build up their human capital through schooling and training. They can also build up their human capital by attracting skilled workers from other countries. If richer countries are able to attract skilled workers, then we will see divergence rather than convergence. [***In Chapter 5 "Globalization and Competitiveness", we discuss how economies actively seek to attract human capital.***]

Turning to technology, divergence in social infrastructure is certainly a possibility. Social infrastructure includes the rule of law, the general business climate, social attitudes toward corruption, the protection of property rights, and many other intangible factors. These influences on economic growth are difficult to define and almost impossible to measure accurately. Yet economists are convinced that successful economies must have a good set of such social institutions. It is likely that it is easier to build and improve such institutions in countries that are relatively prosperous, which would again lead richer countries to grow more rapidly than poorer countries.

Economists have built some of these ideas into the theoretical framework of economic growth. Unfortunately, the models are too complicated for an introductory economics textbook, so we will not go into them in any detail here. We can, however, provide a simple example that conveys the flavor of these more complex ideas. The story goes as follows. We know that workers acquire human capital through education and on-the-job training. Suppose that, when there is more physical capital in the economy (relative to the number of workers), it is easier to acquire human capital. You can study in modern facilities with up-to-date computers. You work with state-of-the-art machinery and become more skilled. In this story, human capital is endogenous: it depends on the amount of physical capital.

To be concrete, imagine that technology is constant, and the amount of human capital is proportional to the amount of physical capital per worker. When we incorporate this assumption into the production function, we end up with a very straightforward relationship:

output = B × physical capital, 

where B is just a number. [***The derivation of this equation is not very difficult; it is explained in the toolkit.***]

In this economy, the ratio of capital stock to GDP is constant at all times (capital/output = 1/B). This economy is always on a balanced-growth path. Because of this, the growth rate of output equals the growth rate of capital stock:

output growth rate = physical capital growth rate. 

The more important point, though, is that this technology does not exhibit diminishing marginal product of capital. The marginal product of capital is constant: it equals B. If this number were different in different economies, then we would expect to see capital stock flowing from economies where B is small toward economies where B is large. We would see divergence rather than convergence.

The model that we have described in this subsection is simplistic. Its point is simply to show that, if we make human capital endogenous, it is much easier to explain divergence. Economists have built more complicated and realistic models with endogenous human capital and technology that give similar results.

***