A comparison of the two amortization methods can be made using the data applicable to the issue of BDCC’s bonds at a discount; $100,000 face value bonds are issued for $90,754, resulting in a discount of $9,246 ($100,000 - $90,754). Under the straight-line method, this $9,246 discount is amortized in equal amounts over the 3-year life of the bonds. The discount is calculated for 6 -month periods, because amortization is recorded at the time that semi-annual interest payments are made. To recap: the straight-line method amortization is calculated as follows:
|
Discount |
$9,246(a) |
|
Number of 6 -month periods remaining |
6(b) |
|
Amortization (a/b) |
$1,541 |
As explained in section C of this chapter, amortization of a discount increases interest expense. Therefore, the $1,541 is added to the $6,000 interest payment to calculate the $7,541 interest expense applicable to each 6 -month period. Under the straight-line method, the effective interest rate varies from period to period.
Under the effective interest method, the amortization of the $9,246 discount each period varies, but the effective interest rate is a constant 4%. Note that the total interest expense of $45,246 for the three-year period is the same under both methods.
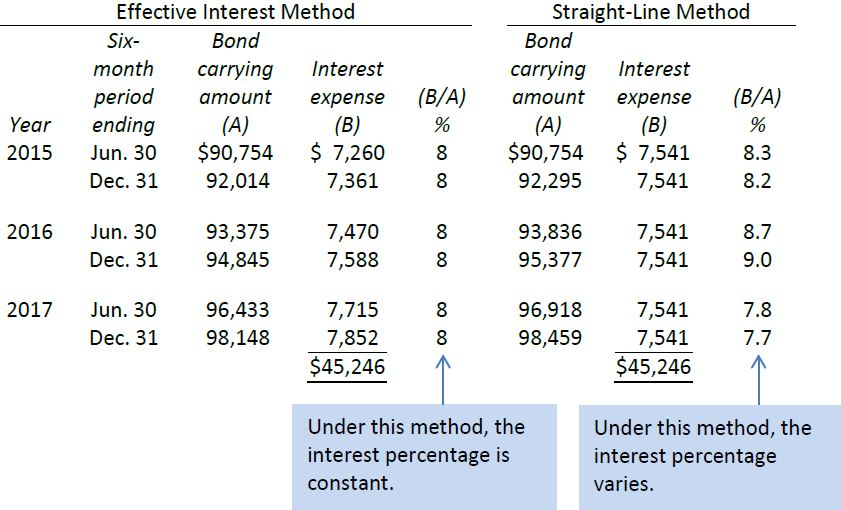
This comparison involved the issue of bonds at a discount. A similar comparison for bonds issued at a premium would indicate a similar difference in the calculation of a periodic financing charge. Under the straight-line method, however, the percentage of financing charge would increase in the case of a premium, rather than decrease as shown here.
- 8374 reads






